REVISION NOTES
IGCSE Edexcel Mathematics A
1.2 Fractions
1.2.1 Understand and use equivalent fractions, simplifying a fraction by cancelling common factors
Simplifying Fractions
- Equivalent fractions: fractions that represent the same value/number
- Fractions can be simplified when the denominator and numerator have common factors other than 1
- The fraction can be simplified by dividing both the denominator and numerator with the greatest common factor (fastest way)
- If greatest common factor is not used, the fraction can also be simplified, but through several steps
- A fraction is in the simplest form if the denominator and numerator have common factor of 1 only
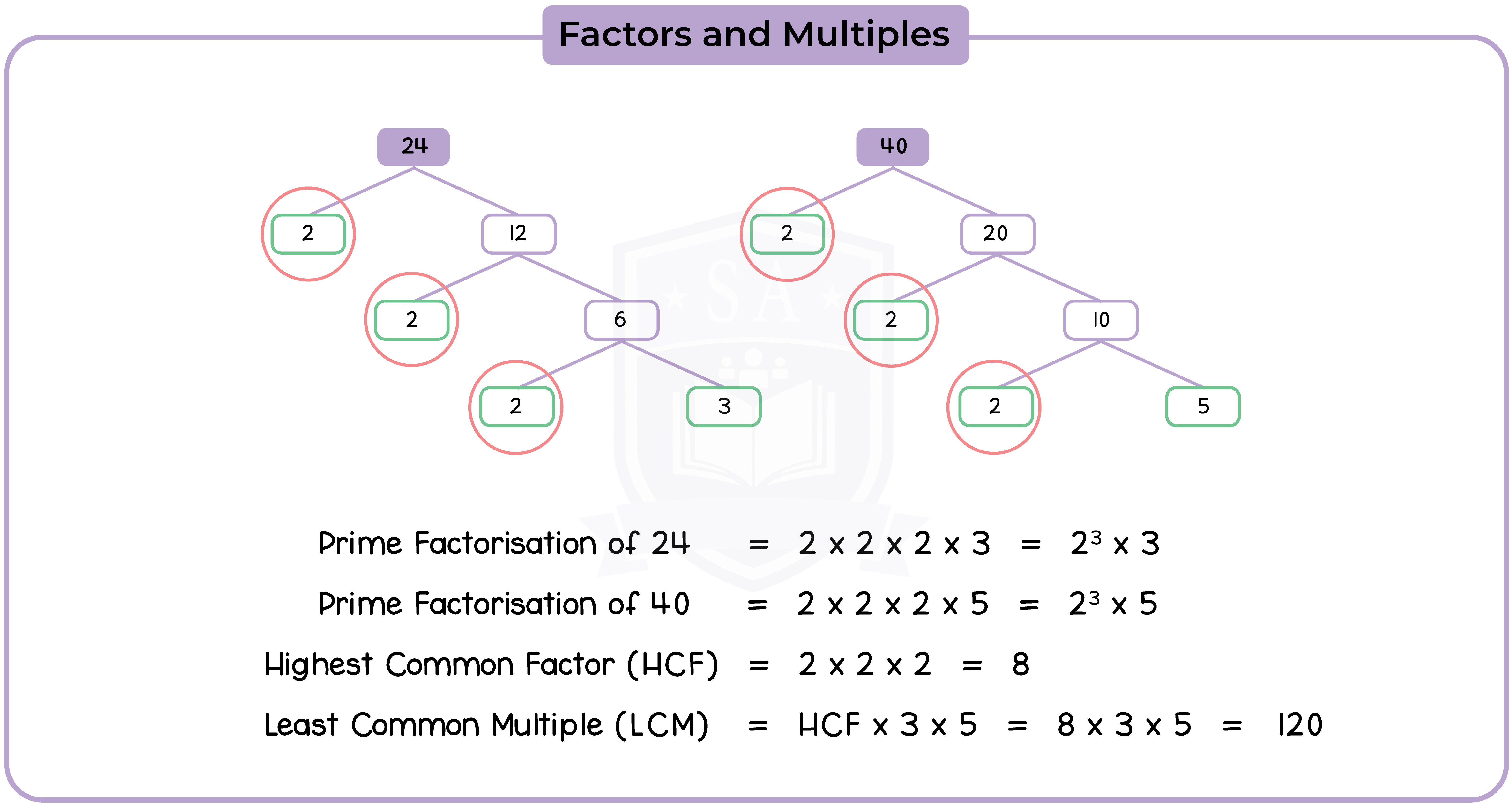
- Another method is to write the denominator and numerator as products of prime factors
- This is especially useful when the numbers are large

1.2.2 Understand and use mixed numbers and vulgar fractions
Vulgar Fractions
- Fractions written in a usual way in which an integer is above another integer separated by a line
- Proper fraction: when the numerator is smaller than the denominator
- Improper fraction: when the numerator is larger than the denominator
Mixed Numbers
- Mixed numbers are made up of a whole number and a proper fraction
From Mixed Numbers to Improper Fractions
From Improper Fractions to Mixed Numbers
1.2.3 Identify common denominators
Common Denominators
- Common denominators should be the common multiples of all denominators
- Usually, we can find the common denominators by multiplying the denominators together
The common denominator of ¾ and ⅔ is 4 x 3 = 12
1.2.4 Order fractions and calculate a given fraction of a given quantity
Equivalent fractions are used to compare the sizes of fractions written with a different denominator
20% = 20/100 = 1/5 = 0.2
1.2.5 Express a given number as a fraction of another number
3.45 = 345/100 = 69/20
1.2.6 Use common denominators to add and subtract fractions and mixed numbers
Type 1: Adding or Subtracting Fractions
Equivalent fractions are also used when adding or subtracting fractions with different denominator.
The fractions must be rewritten to have the same denominator before starting the addition or subtraction.
2/5 + 1/10 = 4/10 + 1/10 = 5/10 = 1/2
Type 2: Adding and Subtracting Mixed Fractions
When adding and subtracting mixed fraction, process the whole number parts separately from the fractions parts, then combine everything at the end.
1.2.7 Convert a fraction to a decimal or a percentage
- 100% = 1,
- therefore ½ = 50% or 0.5
- ¼ = 25% or 0.25
- ⅕ = 20% or 0.2
1.2.8 Understand and use unit fractions as multiplicative inverses
1.2.9 Multiply and divide fractions and mixed numbers
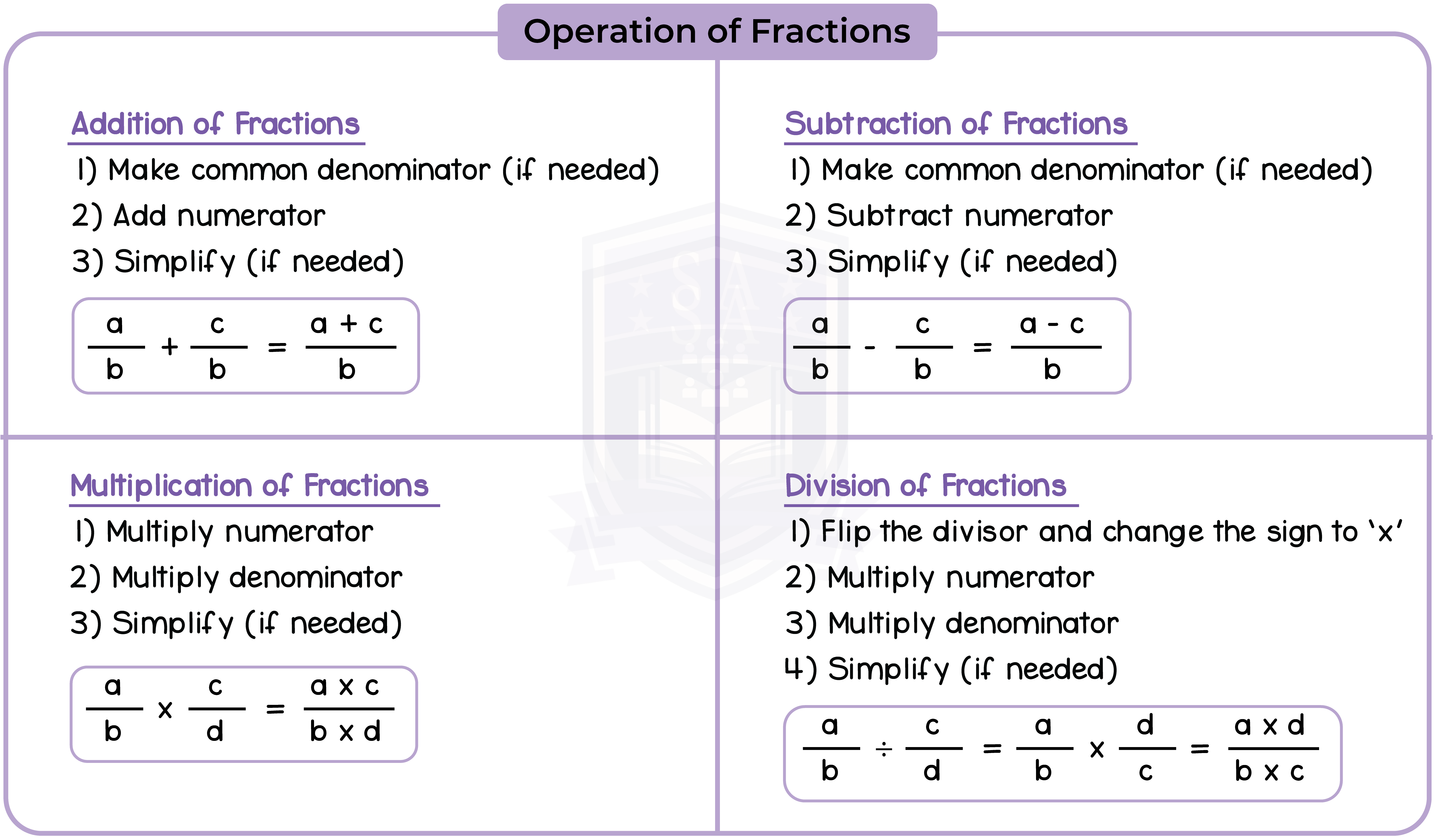
Type 1: Multiplying Fractions
Step 1: Multiply the numerator (top number)
Step 2: Multiply the denominator (bottom number)
Step 3: Simplify (optional)
Type 2: Multiplying Mixed Fractions
Step 1: Convert mixed fractions into improper fractions
Step 2: Multiply the numerator (top number)
Step 3: Multiply the denominator (bottom number)
Step 4: Simplify (optional
Type 3: Dividing Fractions
Step 1: Turn the second fraction upside down
Step 2: Multiply the numerator (top number)
Step 3: Multiply the denominator (bottom number)
Step 4: Simplify (optional)3
Type 4: Dividing Mixed Fractions
Step 1: Turn the second fraction upside down
Step 2: Convert mixed fractions into improper fractions
Step 3: Multiply the numerator (top number)
Step 4: Multiply the denominator (bottom number)
Step 4: Simplify (optional

