REVISION NOTES
3.1.1 Generate terms of a sequence using term-to-term and position-to-term definitions of the sequence
How do I use a position-to-term rule to write the first n terms of a sequence?
How do I use a term-to-term rule to write the first n terms of a sequence?


3.1.2 Find subsequent terms of an integer sequence and the rule for generating it
3.1.3 Use linear expressions to describe the nth term of arithmetic sequences
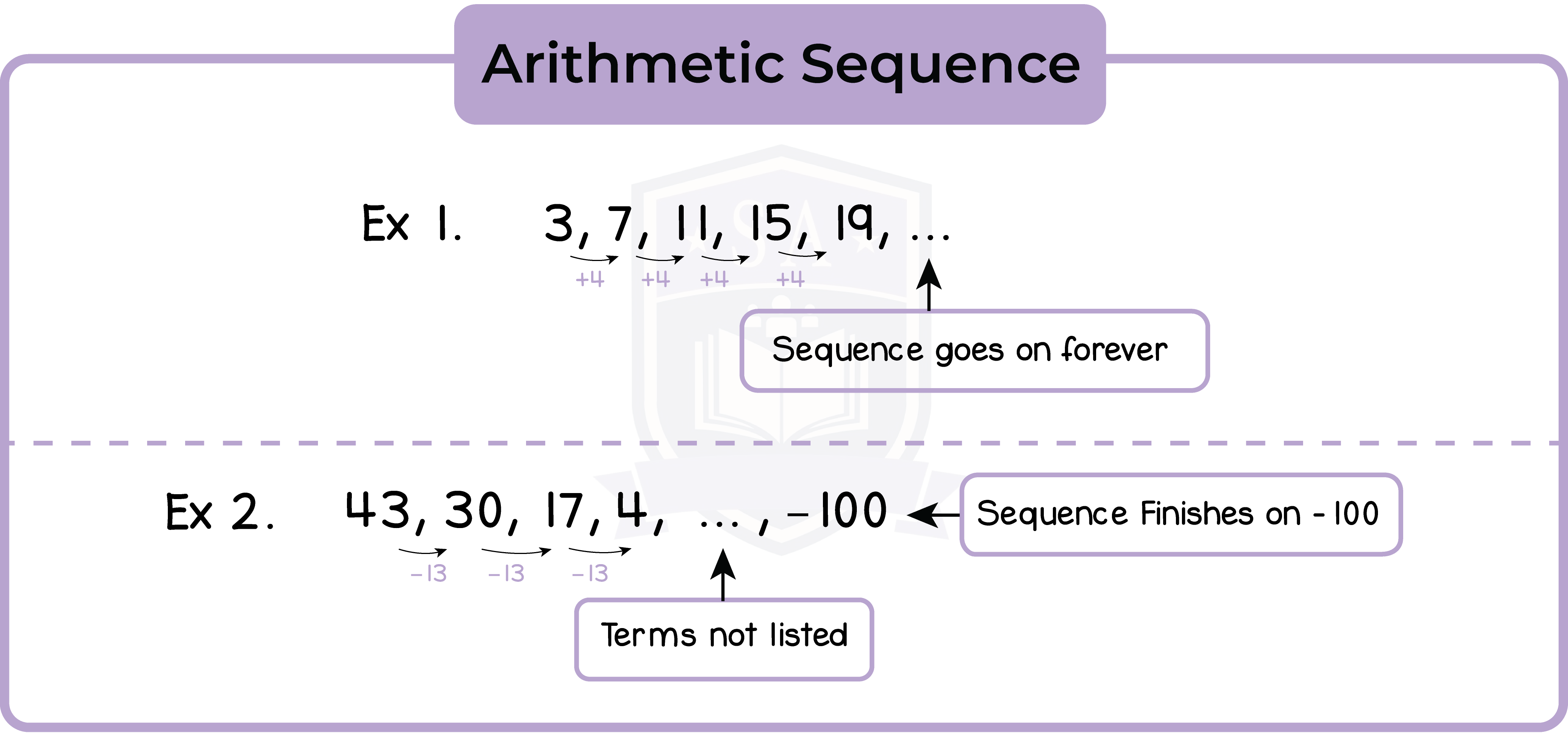
3.1.4 Understand and use common difference (d) and first term (a) in an arithmetic sequence (Higher Tier Only)

3.1.5 Know and use nth term = a + (n – 1) d (Higher Tier Only)
3.1.6 Find the sum of the first n terms of an arithmetic series (Sn) (Higher Tier Only)



© 2025 Studia Academy. All rights reserved.