1.3 Decimals — Studia

REVISION NOTES

IGCSE Edexcel Mathematics A

1.3 Decimals

1.3.1 Use decimal notation

7×10⁶

= 7,000,000

(the decimal point went to the right by 6 digits)

8×10^-4

= 0.0004

(the decimal point went to the left by 4 digits)

1.3.2 Understand place value

What is place value?

When a number is displayed with digits in words, each one of the digits has their own value which is dependant on where it is located within a number
For example in the number 12345.
- 5 = ones
- 4 = tens
- 3 = hundreds
- 2 = thousands
- 1 = ten thousands
So therefore this “12345” in words would be “twelve thousand three hundred forty five”

1.3.3 Order decimals

7 + 0.5 + 0.04 + 0.003+ 0.0002

= 7.5432

8.5 + 0.004+ 0.0005

= 8.5405

1.3.4 Convert a decimal to a fraction or a percentage

Equivalent fractions are used to compare the sizes of fractions written with a different denominator

0.25 = 25% or ¼
0.2 = 20% or ⅕

1.3.5 Express a given number as a fraction of another number

Terminating decimals stop after a finite number of decimal places.

Example: 0.315

Terminating decimals can be written as exact fractions with denominator 10, 100, 1000, etc. and then cancelled down when possible.

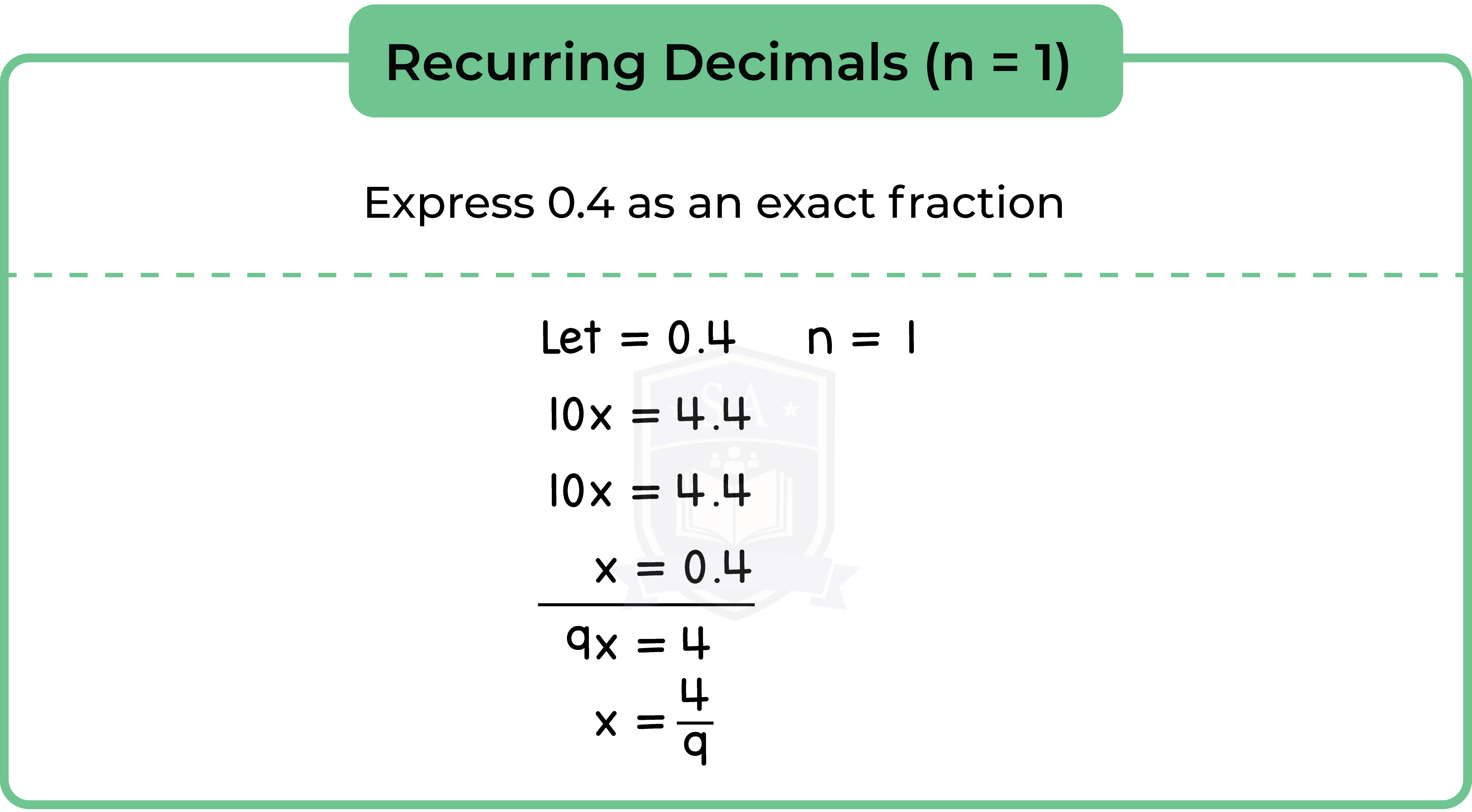
1.3.6 Convert recurring decimals into fractions (Higher Tier Only)

Recurring decimals do not stop after a finite number of decimal places, but they do settle into a patern of digits that repeats indefinitely.

Example: 0.315 315 315 315 315…

Recurring decimals can be written as exact fractions

1. Numbers & the Number System

1.4 Powers and Roots

1.5 Set Language and Notation

1.6 Percentages

1.7 Ratio and Proportion

1.8 Degree of Accuracy

1.9 Standard Form

1.10 Applying Numbers

1.11 Electronic Calculator

2. Equations, Formulae & Identities

2.1 Use of Symbols

2.2 Algebraic Manipulation

2.3 Expressions and Formulae

2.4 Linear Equations

2.5 Proportion (Higher Tier Only)

2.6 Simultaneous Linear Equations

2.7 Quadratic Equations

2.8 Inequalities

3. Sequences, Functions & Graphs

3.2 Function Notation (Higher Tier Only)

3.4 Calculus (Higher Tier Only)

4. Geometry

4.1 Angles, Lines & Triangles

4.5 Construction

4.6 Circle Properties

4.7 Geometric Reasoning

4.8 Trigonometry and Pythagoras’ Theorem

4.9 Mensuration of 2D Shapes

4.10 3D Shapes and Volumes

4.11 Similarity

5. Vectors & Transformation Geometry

5.1 Vectors (Higher Tier Only)

5.2 Transformation Geometry

6. Statistics & Probability

6.1 Graphical Representation of Data

6.2 Statistical Measures

6.3 Probability

7. Appendix

7.1 Appendix 1: Foundation Tier Formula Sheet (Given)

7.2 Appendix 2: Foundation Tier Formula Sheet (To Memorise)

7.3 Appendix 3: Higher Tier Formula Sheet (Given)

7.4 Appendix 4: Higher Tier Formula Sheet (To Memorise)

7.5 Appendix 5: Notation