REVISION NOTES

IGCSE Edexcel Mathematics A

1.2 Fractions

1.2.1 Understand and use equivalent fractions, simplifying a fraction by cancelling common factors

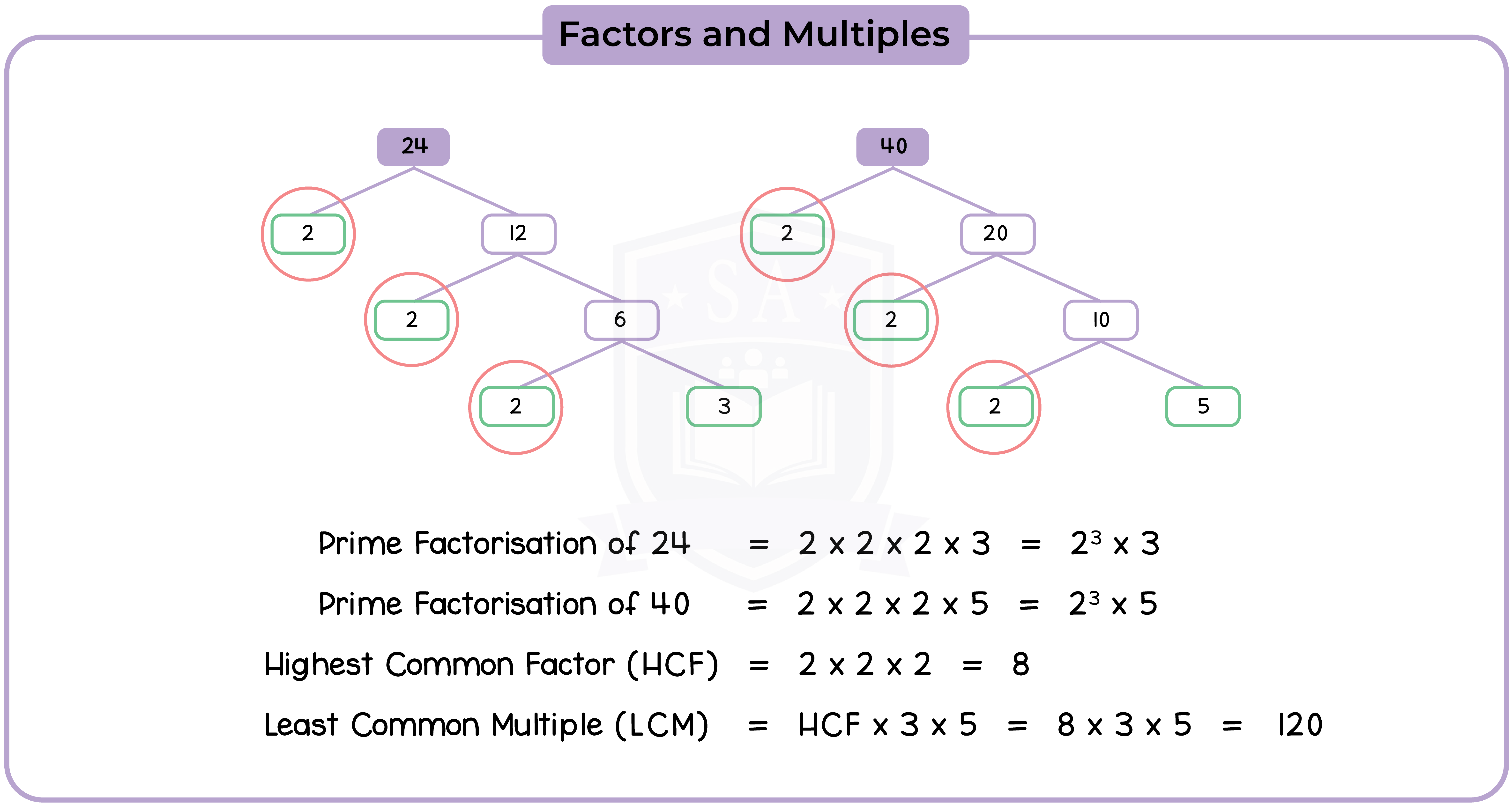
Simplifying Fractions

  • Equivalent fractions: fractions that represent the same value/number
  • Fractions can be simplified when the denominator and numerator have common factors other than 1
    • The fraction can be simplified by dividing both the denominator and numerator with the greatest common factor (fastest way)
    • If greatest common factor is not used, the fraction can also be simplified, but through several steps
  • A fraction is in the simplest form if the denominator and numerator have common factor of 1 only
  • Another method is to write the denominator and numerator as products of prime factors
  • This is especially useful when the numbers are large
edexcel_igcse_mathematics a_topic 02_fractions_001_equivalent fraction
edexcel_igcse_mathematics a_topic 02_fractions_002_factors and multiples

1.2.2 Understand and use mixed numbers and vulgar fractions

Vulgar Fractions

  • Fractions written in a usual way in which an integer is above another integer separated by a line
    • Proper fraction: when the numerator is smaller than the denominator
    • Improper fraction: when the numerator is larger than the denominator

Mixed Numbers

  • Mixed numbers are made up of a whole number and a proper fraction

From Mixed Numbers to Improper Fractions

From Improper Fractions to Mixed Numbers

1.2.3 Identify common denominators

Common Denominators

  • Common denominators should be the common multiples of all denominators
  • Usually, we can find the common denominators by multiplying the denominators together

The common denominator of ¾ and ⅔ is 4 x 3 = 12

1.2.4 Order fractions and calculate a given fraction of a given quantity

Equivalent fractions are used to compare the sizes of fractions written with a different denominator

20% = 20/100 = 1/5 = 0.2

1.2.5 Express a given number as a fraction of another number

3.45 = 345/100 = 69/20

1.2.6 Use common denominators to add and subtract fractions and mixed numbers

Type 1: Adding or Subtracting Fractions

Equivalent fractions are also used when adding or subtracting fractions with different denominator.

The fractions must be rewritten to have the same denominator before starting the addition or subtraction.

 

2/5 + 1/10 = 4/10 + 1/10 = 5/10 = 1/2

Type 2: Adding and Subtracting Mixed Fractions

When adding and subtracting mixed fraction, process the whole number parts separately from the fractions parts, then combine everything at the end.

1.2.7 Convert a fraction to a decimal or a percentage

  • 100% = 1,
  • therefore ½ = 50% or 0.5
  • ¼ = 25% or 0.25
  • ⅕ = 20% or 0.2

1.2.8 Understand and use unit fractions as multiplicative inverses

1.2.9 Multiply and divide fractions and mixed numbers

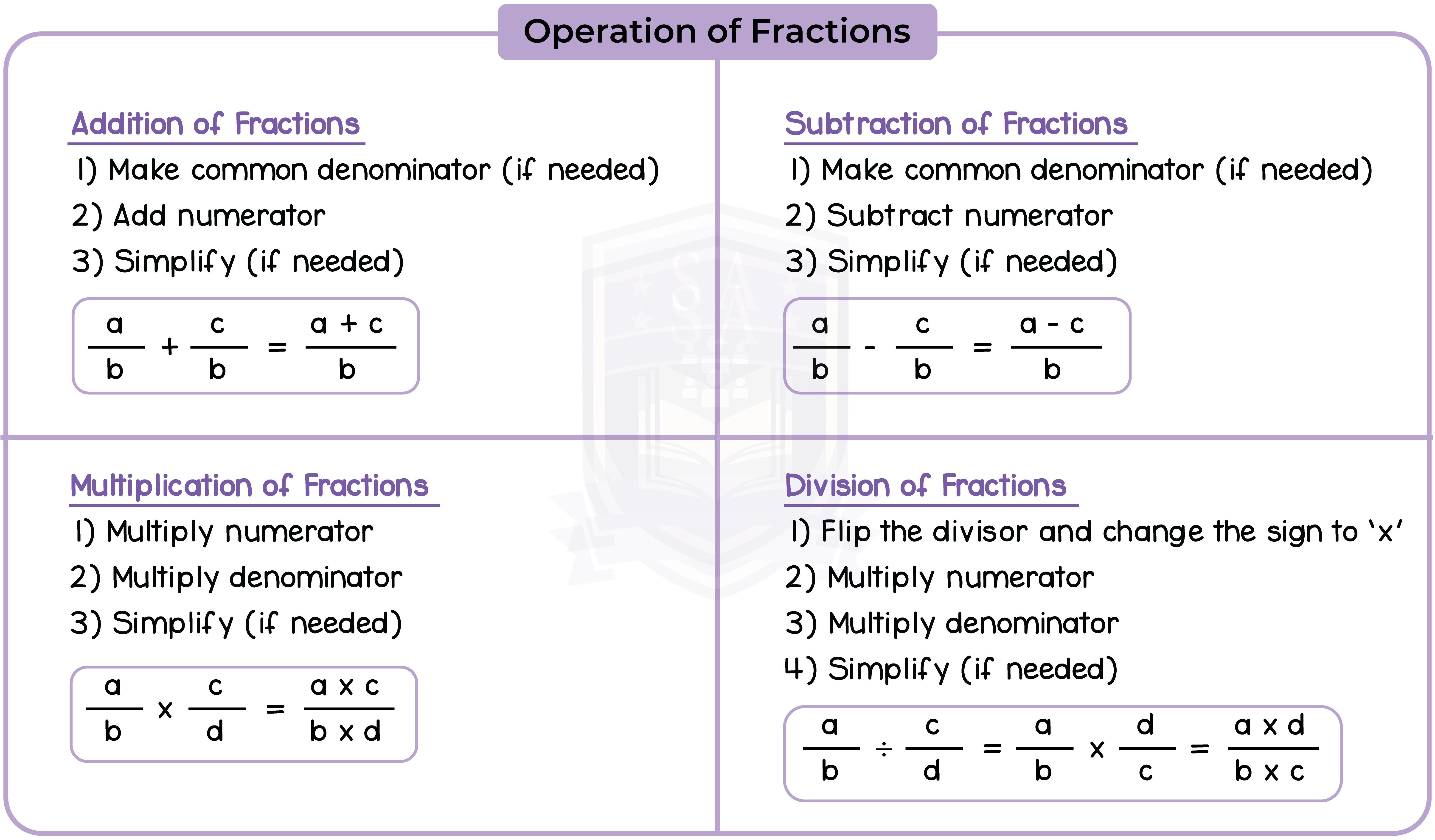
edexcel_igcse_mathematics a_topic 02_fractions_003_operation of fraction
edexcel_igcse_mathematics a_topic 02_fractions_004_operation of fraction

Type 1: Multiplying Fractions

Step 1: Multiply the numerator (top number)

Step 2: Multiply the denominator (bottom number)

Step 3: Simplify (optional)

Type 2: Multiplying Mixed Fractions

Step 1: Convert mixed fractions into improper fractions

Step 2: Multiply the numerator (top number)

Step 3: Multiply the denominator (bottom number)

Step 4: Simplify (optional

Type 3: Dividing Fractions

Step 1: Turn the second fraction upside down

Step 2: Multiply the numerator (top number)

Step 3: Multiply the denominator (bottom number)

Step 4: Simplify (optional)3

Type 4: Dividing Mixed Fractions

Step 1: Turn the second fraction upside down

Step 2: Convert mixed fractions into improper fractions

Step 3: Multiply the numerator (top number)

Step 4: Multiply the denominator (bottom number)

Step 4: Simplify (optional

Back
Next

1.1 Integers

1.2 Fractions

1.3 Decimals

1.4 Powers and Roots

1.5 Set Language and Notation

1.6 Percentages

1.7 Ratio and Proportion

1.8 Degree of Accuracy

1.9 Standard Form

1.10 Applying Numbers

1.11 Electronic Calculator

2.1 Use of Symbols

2.2 Algebraic Manipulation

2.3 Expressions and Formulae

2.4 Linear Equations

2.5 Proportion (Higher Tier Only)

2.6 Simultaneous Linear Equations

2.7 Quadratic Equations

2.8 Inequalities

3.1 Sequences

3.2 Function Notation (Higher Tier Only)

3.3 Graphs

3.4 Calculus (Higher Tier Only)

4.1 Angles, Lines & Triangles

4.2 Polygons

4.3 Symmetry

4.4 Measures

4.5 Construction

4.6 Circle Properties

4.7 Geometric Reasoning

4.8 Trigonometry and Pythagoras’ Theorem

4.9 Mensuration of 2D Shapes

4.10 3D Shapes and Volumes

4.11 Similarity

5.1 Vectors (Higher Tier Only)

5.2 Transformation Geometry

6.1 Graphical Representation of Data

6.2 Statistical Measures

6.3 Probability

7.1 Appendix 1: Foundation Tier Formula Sheet (Given)

7.2 Appendix 2: Foundation Tier Formula Sheet (To Memorise)

7.3 Appendix 3: Higher Tier Formula Sheet (Given)

7.4 Appendix 4: Higher Tier Formula Sheet (To Memorise)

7.5 Appendix 5: Notation

Start Your Success Story Today

© 2025 Studia Academy. All rights reserved.

  • Terms of Use
  • Privacy Policy

Contact Studia

Please fill out the form below, and we’ll get back to you as soon as possible.