REVISION NOTES
IGCSE Edexcel Further Pure Mathematics
1.7 Scalar and Vector Quantities


1.7.1 The addition and subtraction of coplanar vectors and the multiplication of a vector by a scalar
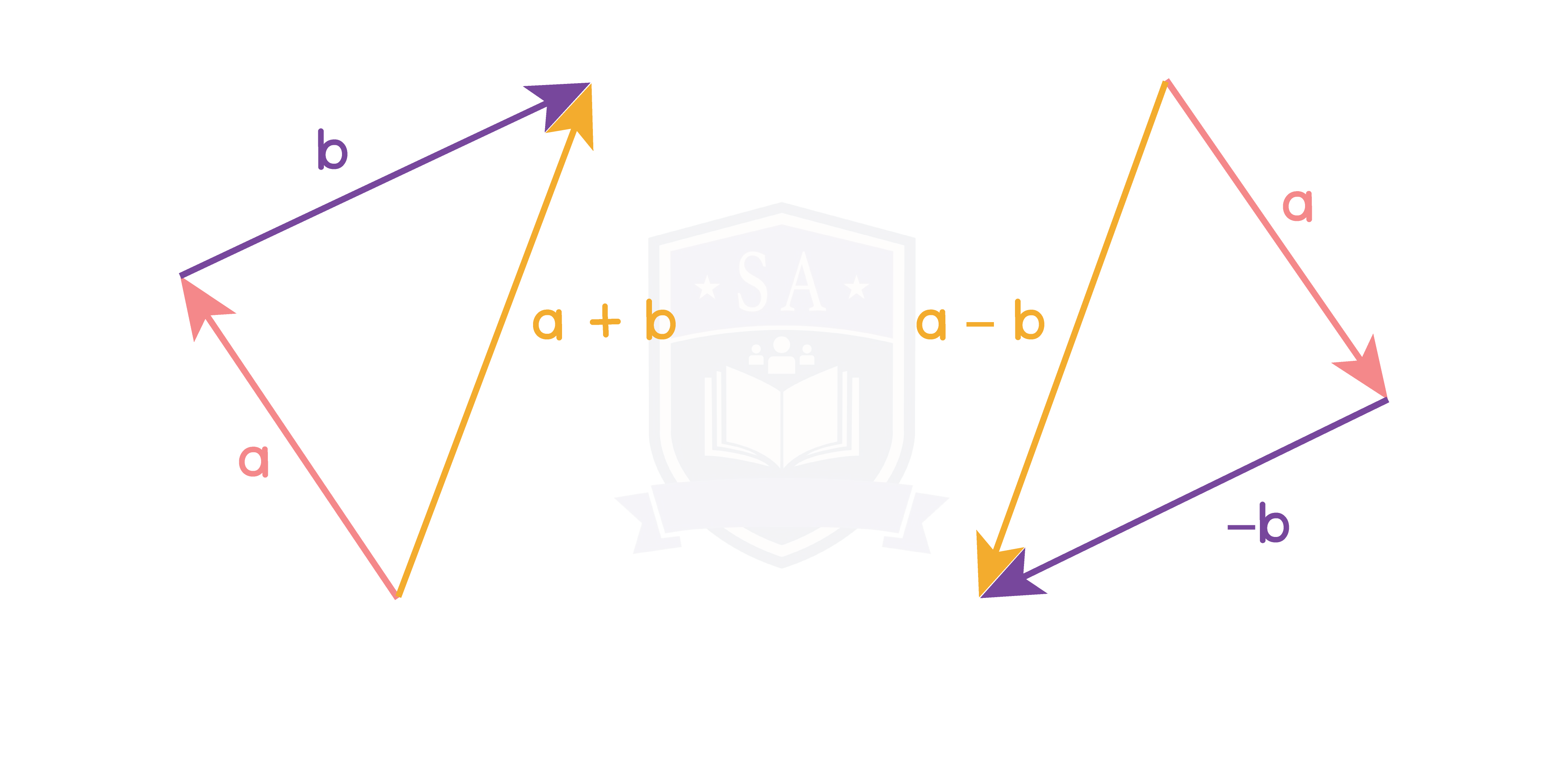
Part 1: Addition and Subtraction of Coplanar vectors
Two vectors are added or subtracted using the ‘triangle law’:
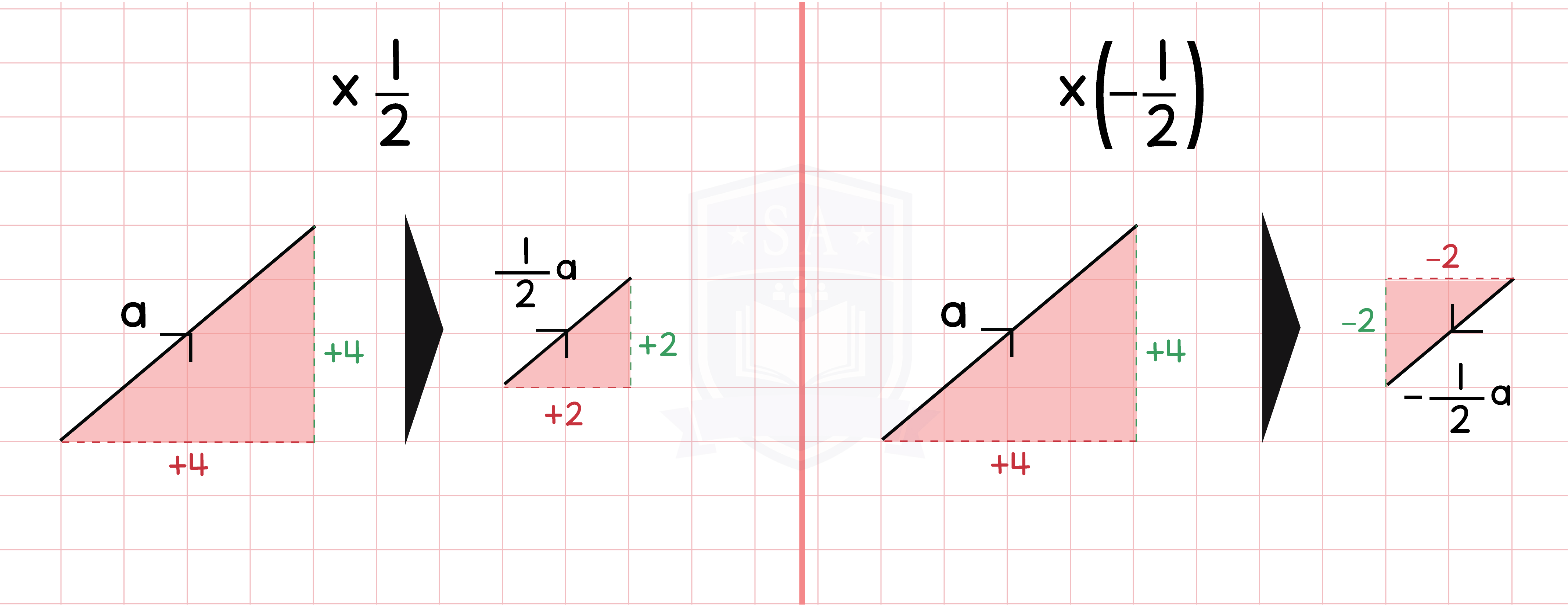
Part 2: Multiplication of a Vector by a Scalar
Type 1: k = 1
The vector -a has the same magnitude as the vector a but is in the opposite direction.

Type 2: k > 1
Type 3: k < 1
1.7.2 Components and resolved parts of a vector

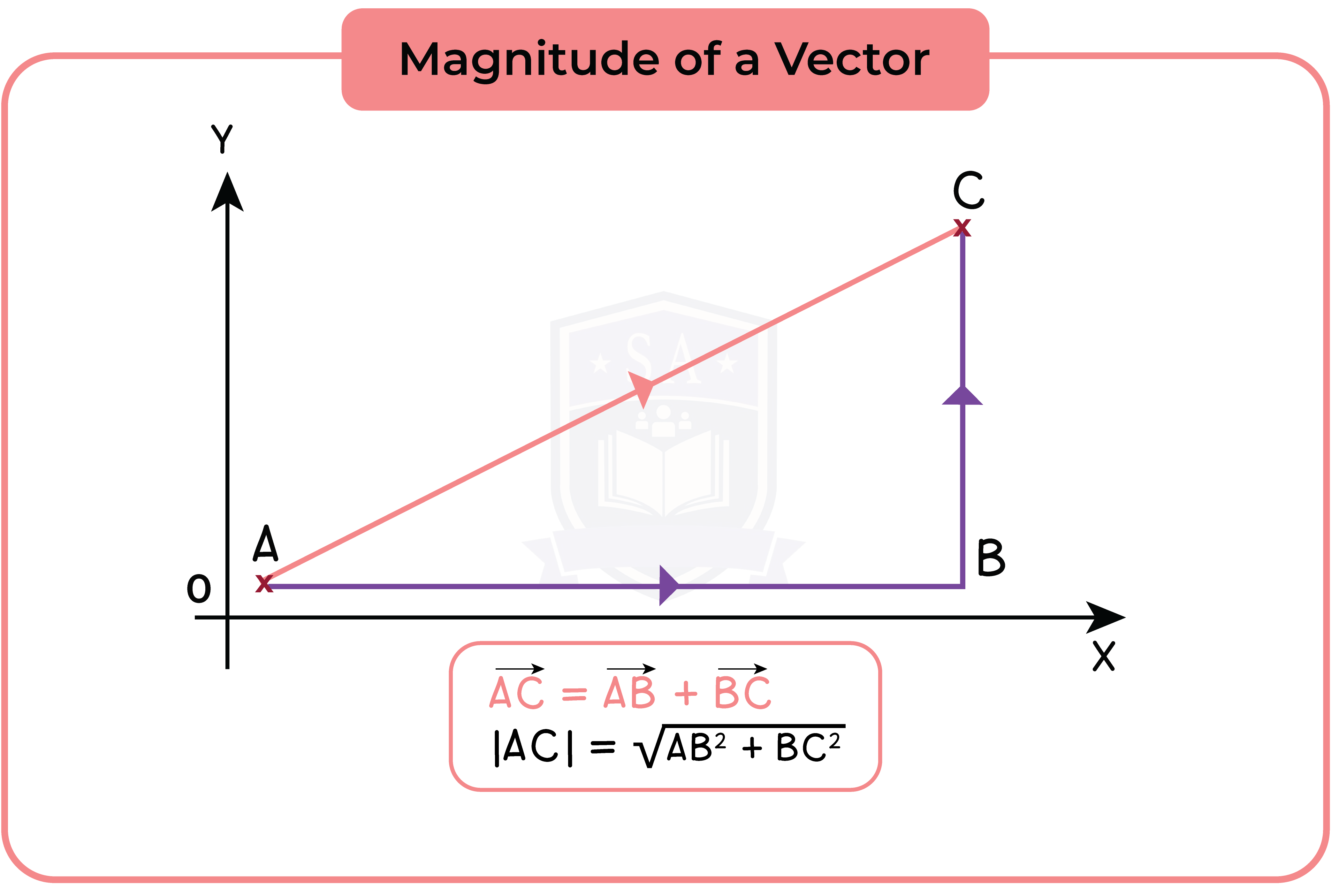
1.7.3 Magnitude of a vector
In geometry, magnitude of a vector means the distance of the vector.
To find the magnitude of a vector, use Pythagoras’ Theorem.
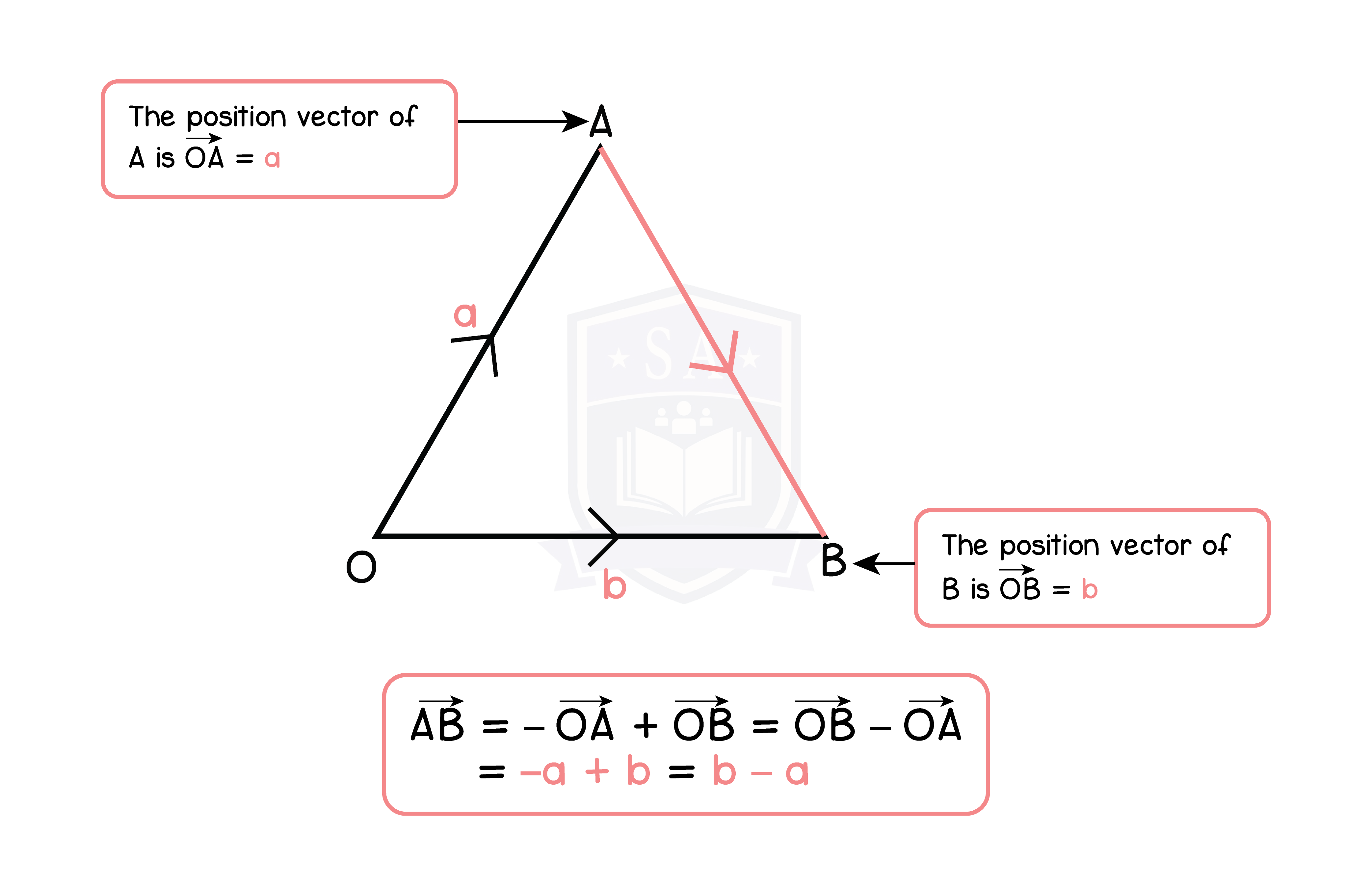
1.7.4 Position vector
The position vector of a point A is the vector OA, where O is the origin. OA is usually written as a vector a.

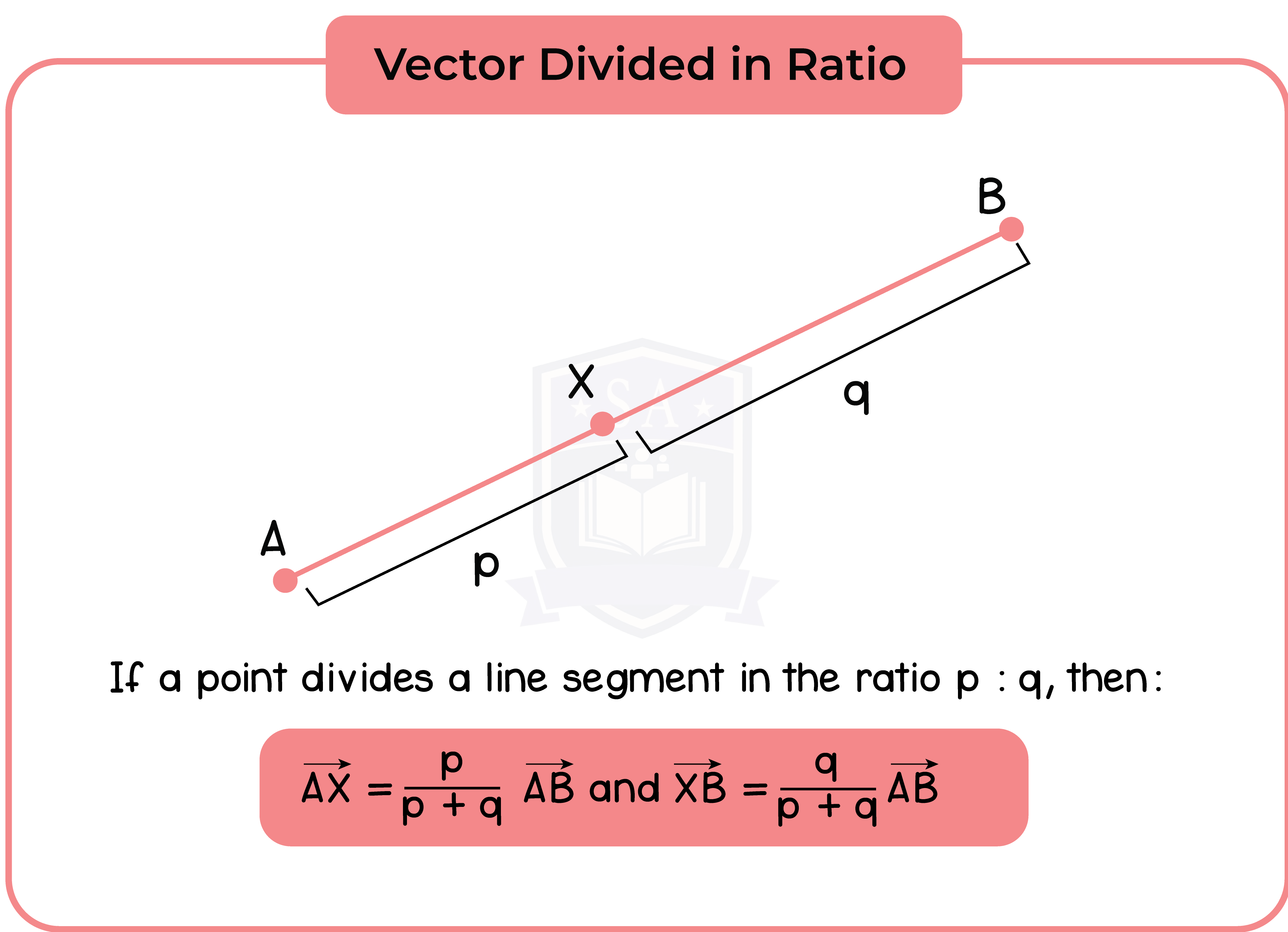
The position of A and B, AB = b – a
1.7.5 Unit vector
A unit vector is a vector which has magnitude 1 unit.

1.7.6 Use of vectors to establish simple properties of geometrical figures
If λa + µb = αa + βb are not parallel, then λ = α and µ = β.
Proof 1: Parallel Line
Condition: If AB = k CD, AB and CD are parallel.
For example, 6a + 3b is parallel to 2a + b, since 6a + 3b = 3 x (2a + b)
Proof 2: Straight Line
Condition 1: If AB = k CD, AB and CD are parallel.
Condition 2: Since both AB and BC go through common point B, therefore ABC is a straight line.