Login
Join Now

REVISION NOTES

IGCSE Edexcel Further Pure Mathematics

Home / Resources / IGCSE / Further Pure Mathematics / Revision Notes / 1.6 The Binomial Series
a

1.6 The Binomial Series

1.6.1 Use of the binomial series (1 + x)n

edexcel_igcse_further pure maths_fpm_topic 06_the binomial series_001_binomial series.png
edexcel_igcse_further pure maths_fpm_topic 06_the binomial series_002_combination formula.png

Type 1: Binomial Expansion (n is a positive integer)

edexcel_igcse_further pure maths_fpm_topic 06_the binomial series_003_binomial expansion (n is a positive integer).png

Type 2: Binomial Expansion (n is a negative integer)

When n is a negative integer, none of the (n – r) terms in the coefficient will be equal to zero, so the series will be infinite.

edexcel_igcse_further pure maths_fpm_topic 06_the binomial series_004_binomial expansion (n is a negative integer).png

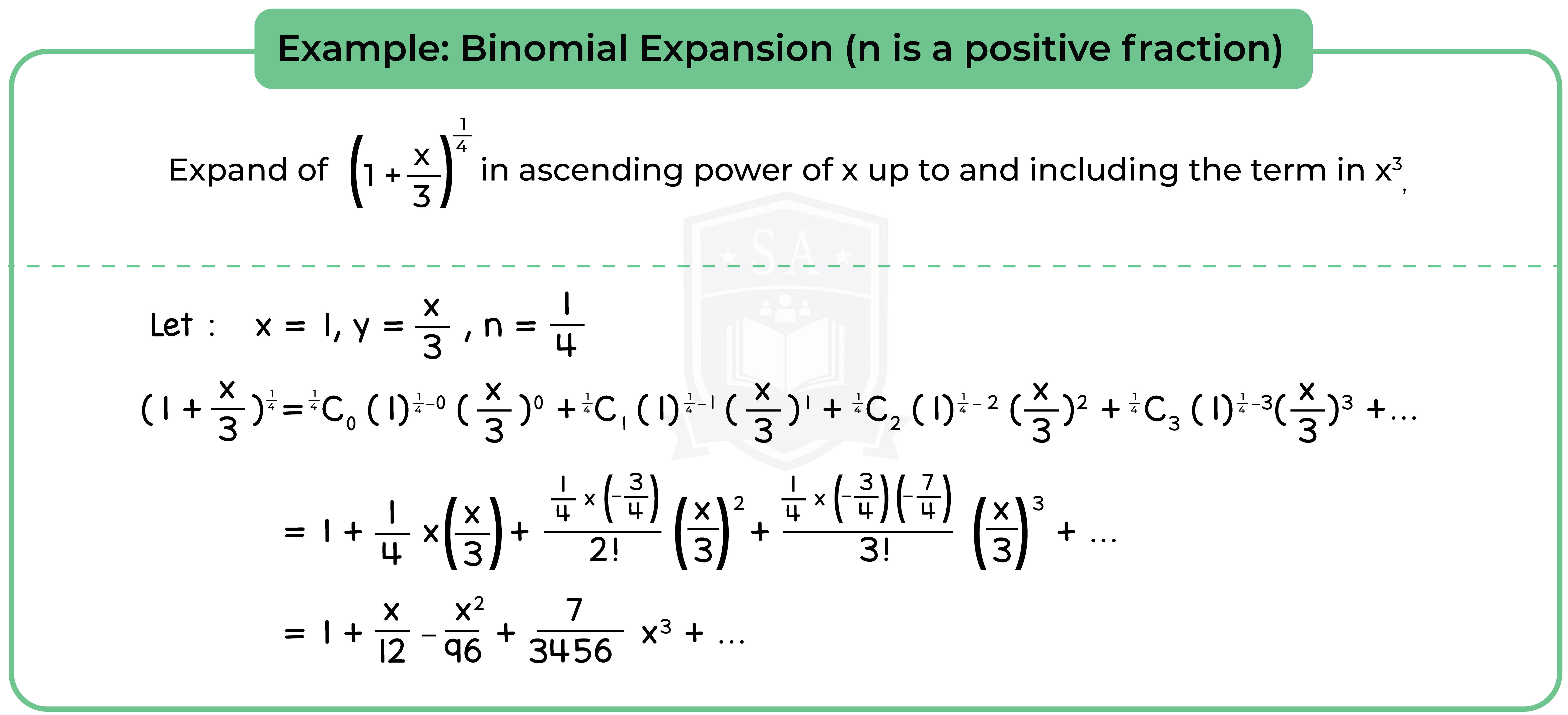
Type 3: Binomial Expansion (n is a positive fractions)

edexcel_igcse_further pure maths_fpm_topic 06_the binomial series_005_binomial expansion (n is a positive fraction).png

Type 3: Binomial Expansion (n is a negative fraction)

edexcel_igcse_further pure maths_fpm_topic 06_the binomial series_006_binomial expansion (n is a negative fraction).png
Back
Next

1.1 Logarithmic Functions and Indices

1.2 The Quadratic Function

1.3 Identities and Inequalities

1.4 Graphs

1.5 Series

1.6 The Binomial Series

1.7 Scalar and Vector Quantities

1.8 Rectangular Cartesian Coordinates

1.9 Calculus

1.10 Trigonometry

Ready to be a Part of Studia Academy?

It’s never too late to start your learning journey with us!

Join Now

Studia Academy © 2023. All Rights Reserved