REVISION NOTES
IGCSE Edexcel Further Pure Mathematics
1.5 Series
1.5.1 Use of the ∑ notation

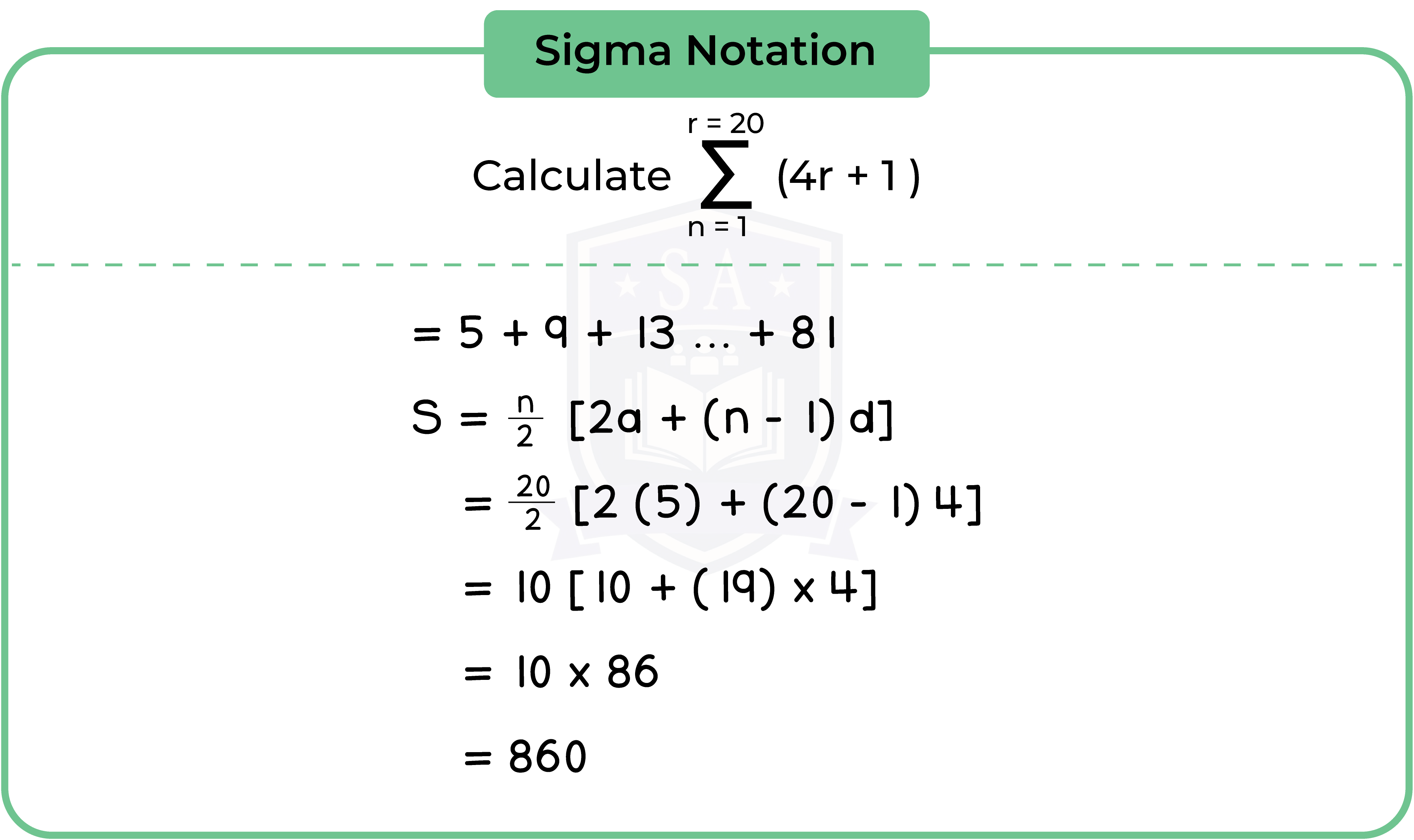
Find sum when lower limit is NOT 1:
Supper limit – Slower limit – 1
1.5.2 Arithmetic and geometric series
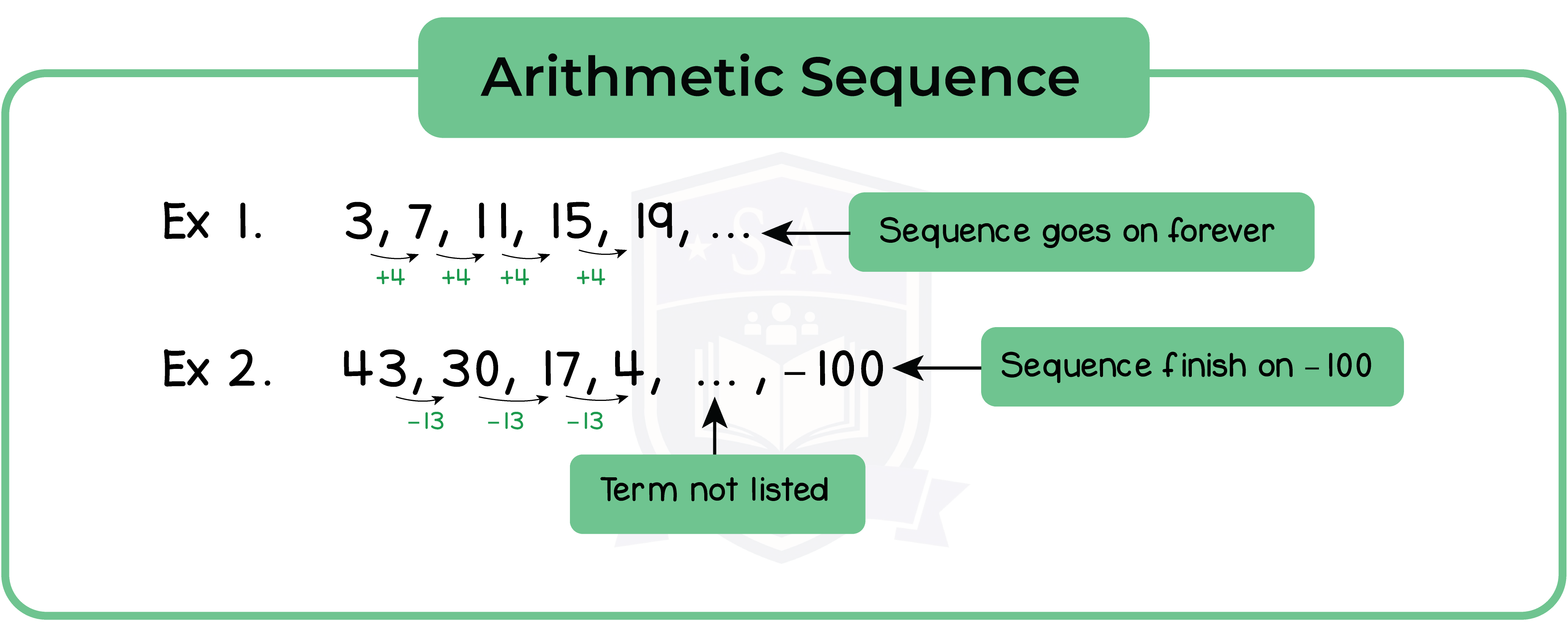
Arithmetic Sequence
An arithmetic sequence is a sequence of numbers that increase or decrease by the same amount. This amount is called common difference.


Arithmetic Series
An arithmetic series is the sum of the terms in an arithmetic sequence.


Geometric Sequence
A geometric sequence is a sequence of numbers that increase or decrease by a common ratio.


Geometric Series
An geometric series is the sum of the terms in an geometric sequence.
Type 1: Geometric Series (Finite)



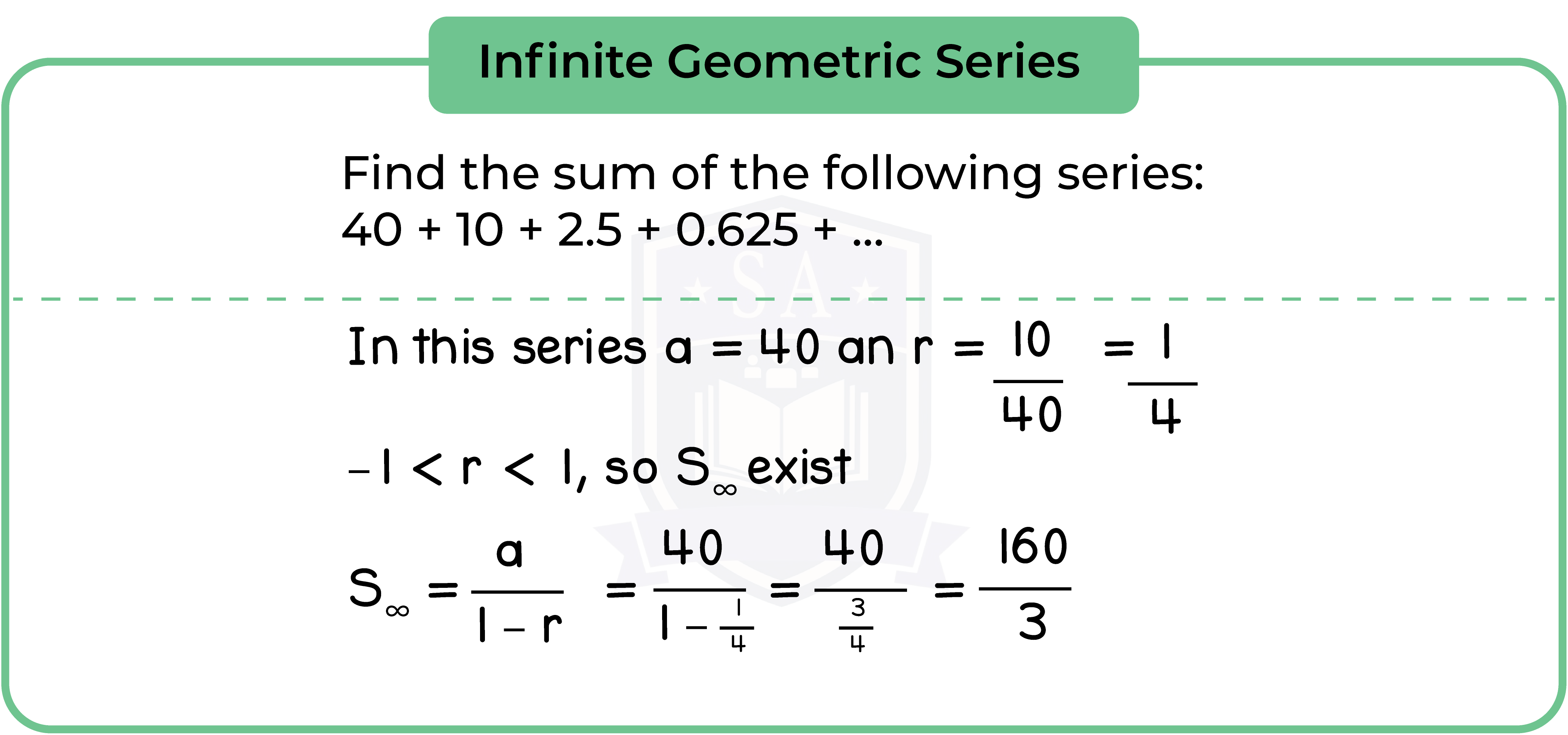
Type 2: Geometric Series (Infinite)
If |r| < 1, then rn approaches 0 for very large n.
We say that the series converges. We call this the limiting sum of the series.