REVISION NOTES
IGCSE Edexcel Further Pure Mathematics
1.4 Graphs
1.4.1 Graphs of polynomials and rational functions with linear denominators
Linear Function
Step 1: Plot the y-intercept
Step 2: Use the gradient to find the second coordinate
Step 3: Sketch the linear function
Don’t forget to label the x-axis, x- intercept, y-intercept.

Quadratic Function
Step 1: Find the y-intercept (x = 0)
Step 2: Find the x-intercept (y = 0) by solving the cubic function [Topic 2]
Step 3: Sketch the quadratic function
Don’t forget to label the x-axis, x- intercept, y-intercept, and turning point.
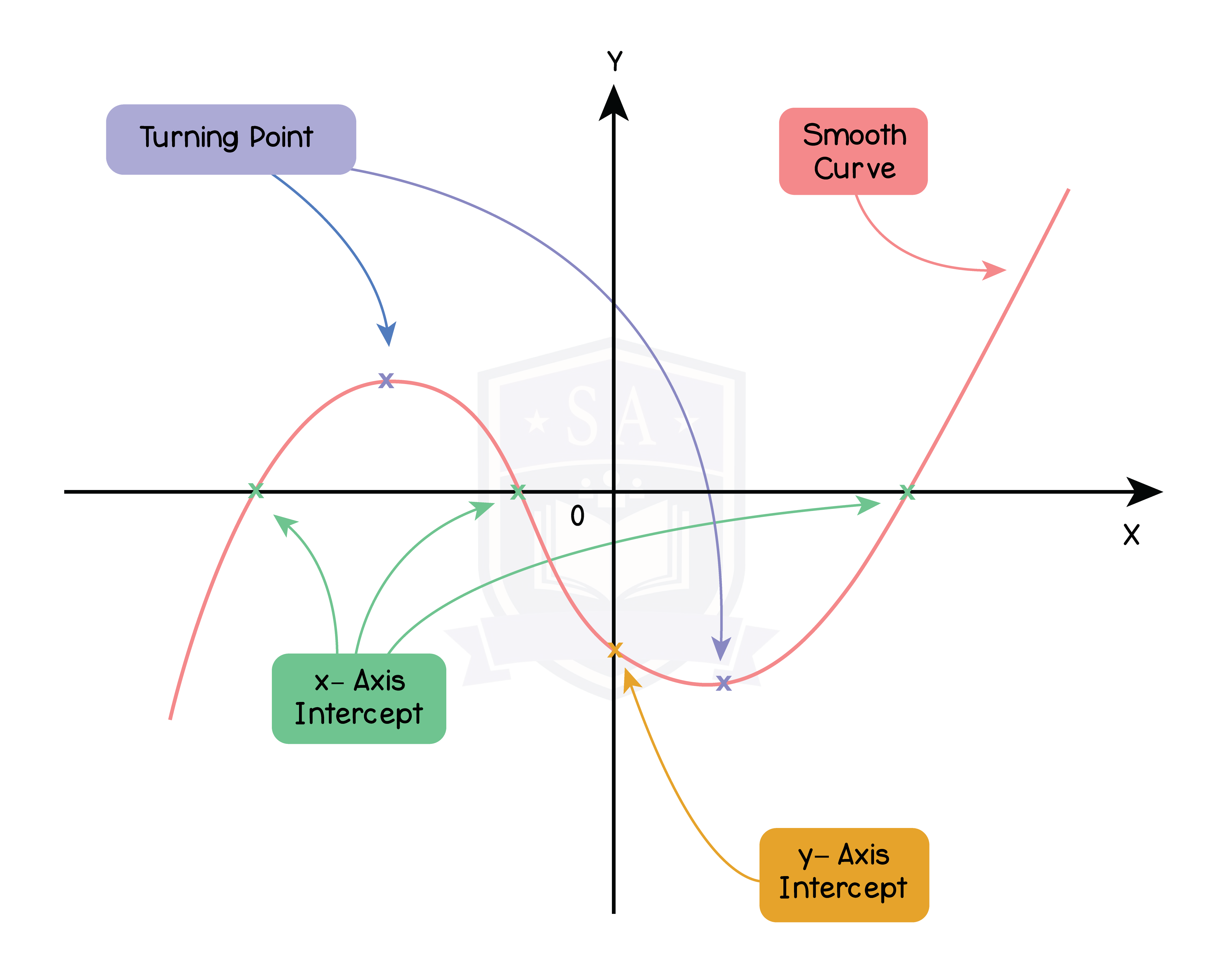
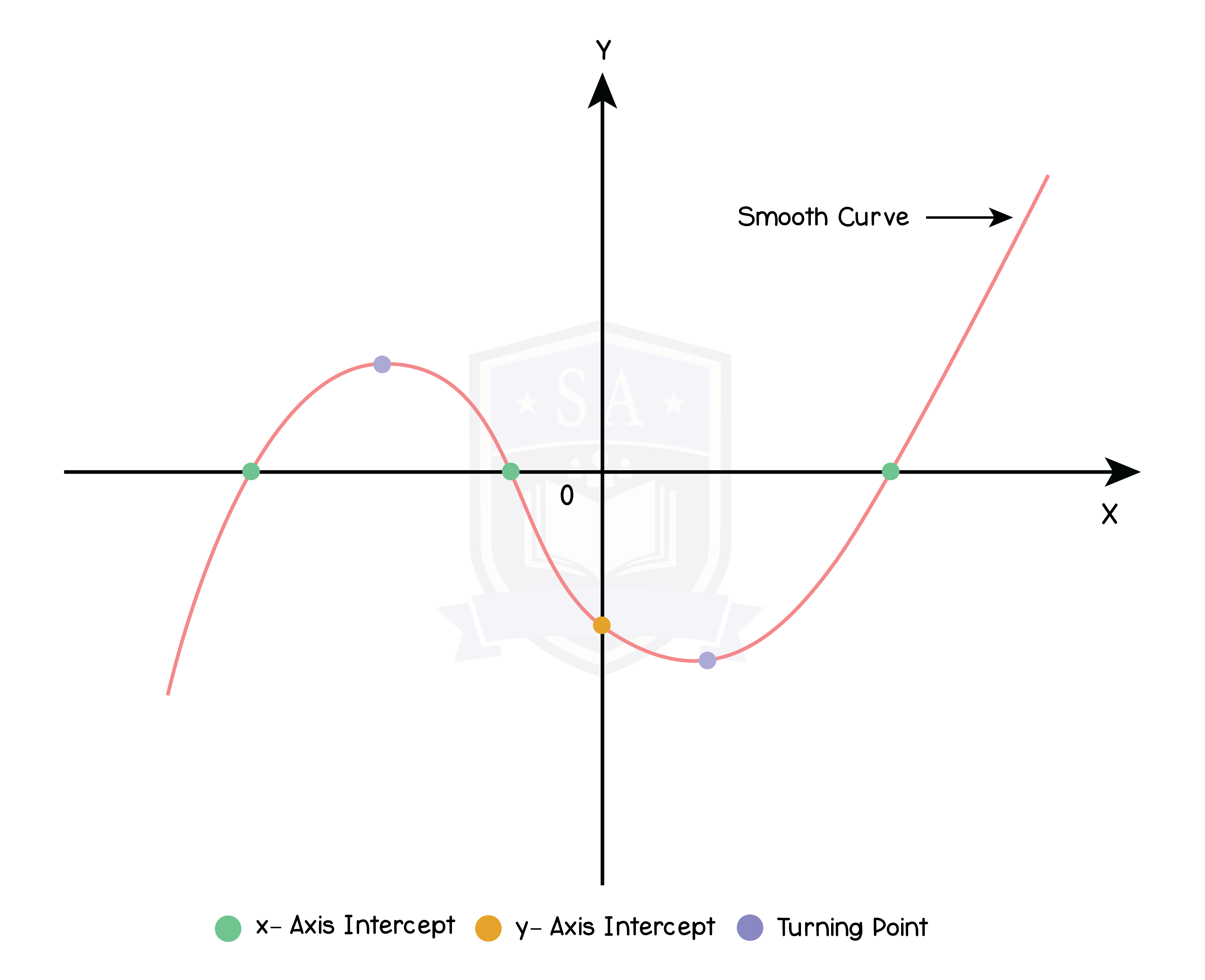
Cubic Functions
Step 1: Find the y-intercept (x = 0)
Step 2: Find the x-intercept (y = 0) by solving the cubic function [Topic 3 Part 2]
Step 3: Find the turning point by completing the square or differentiation
Step 4: Sketch the cubic function
Don’t forget to label the x-axis, x- intercept, y-intercept, and turning point.
Reciprocal Function
Sketching Reciprocal Function
Step 1: Determine the location of the curve (Positive – Quadrant 1 and 3) (Negative – Quadrant 2 and 4)
Step 2: Draw the asymptotes with a dotted line
- Horizontal Asymptote
- If the power of numerator < power of denominator, horizontal asymptote is the x-axis (y = 0)
- If the power of numerator = power of denominator, horizontal asymptote is y = numerator leading coefficient / denominator leading coefficient
- If the power of numerator > power of denominator, there is no horizontal asymptote
- Vertical Asymptote
- The denominator of a fraction cannot be 0
- Square root cannot be less than 0
Step 3: Sketch the reciprocal function
Don’t forget to label the axis, x-intercept, y-intercept, horizontal asymptote, and vertical asymptote.

Exponential and Logarithmic Function
Exponential and logarithmic graph is a reflection with y = x.

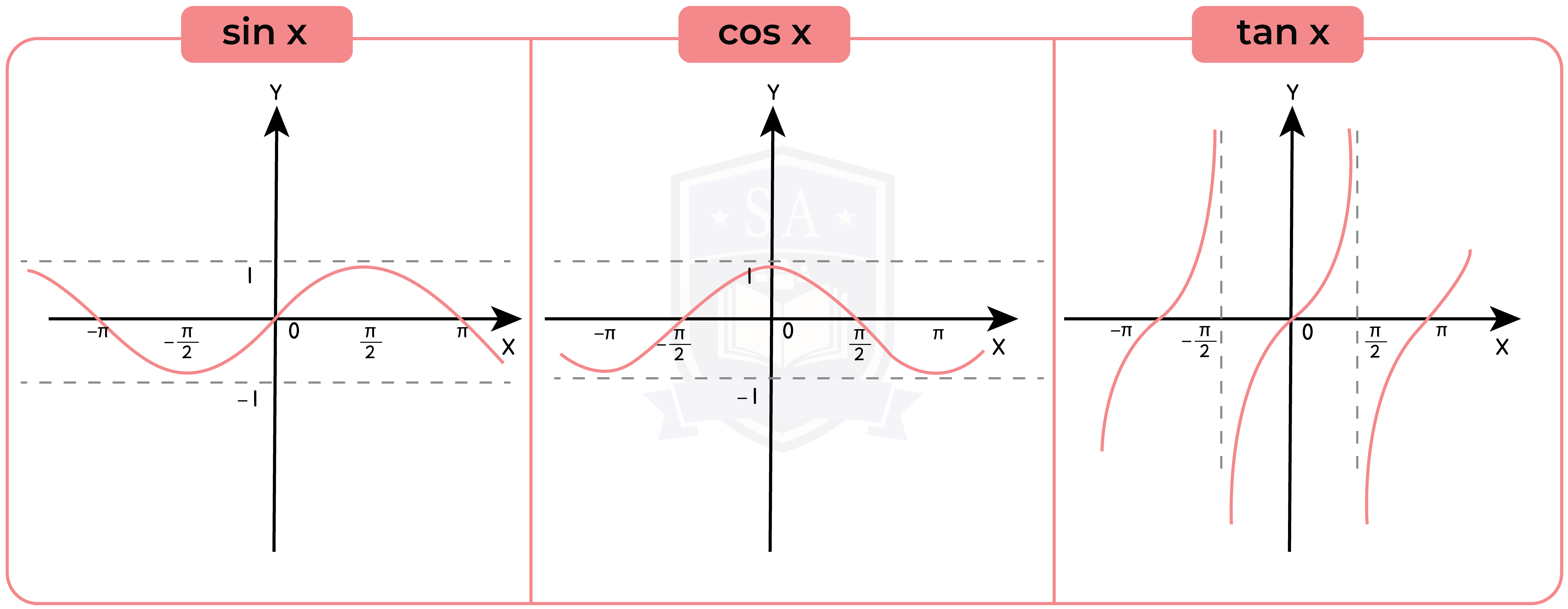
Trigonometric Function
Sin and Cos graph is periodic with a period of 360o . Tan graph is periodic with a period of 180o .
Graph Transformation
f(x + a) is a horizontal translation of – a
f(x) + a is a vertical translation of + a
f(ax) is a horizontal stretch of a scale factor 1/a
af(x) is a vertical stretch of scale factor a
1.4.2 The solution of equations and transcendental functions by graphical methods
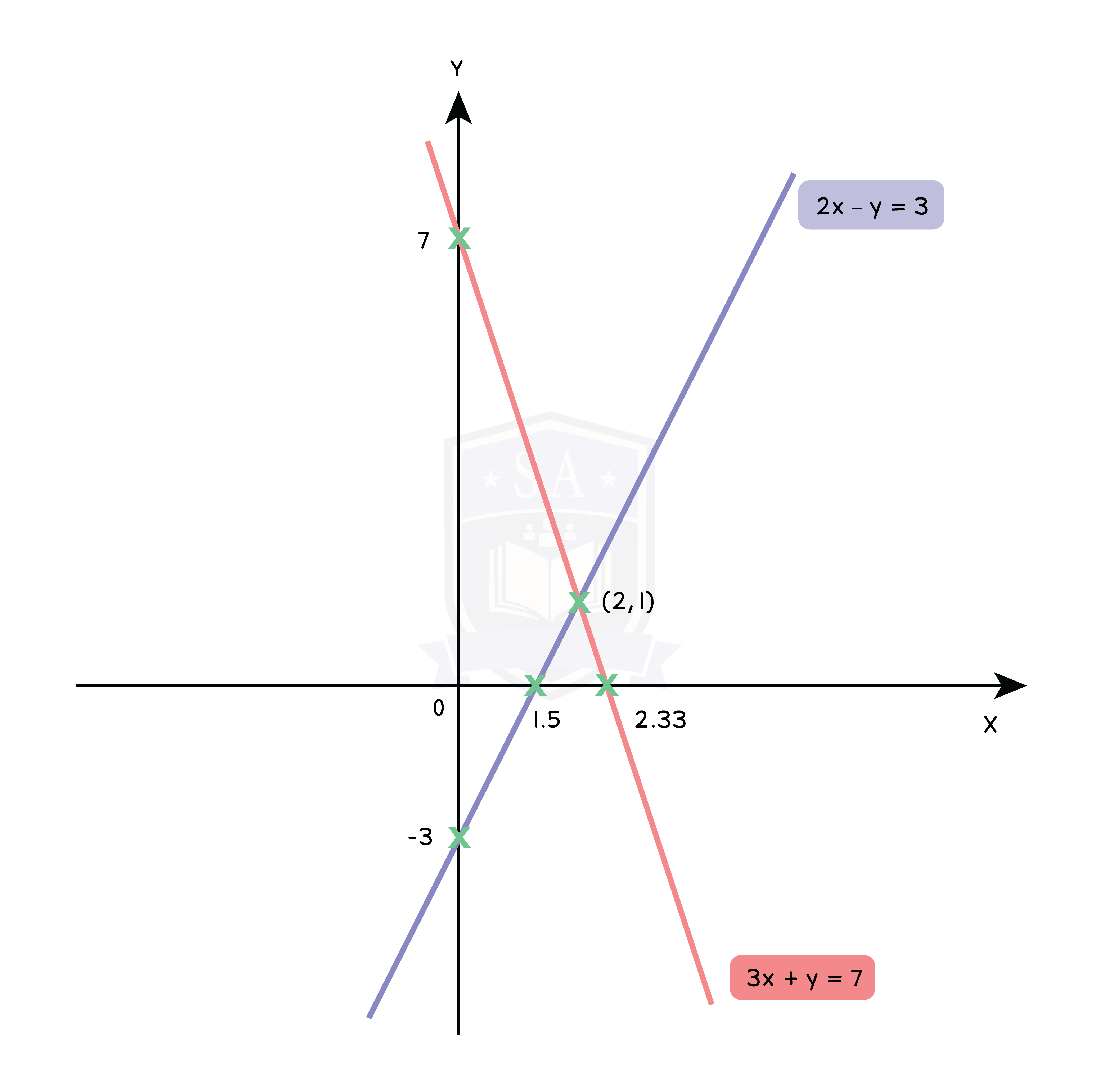
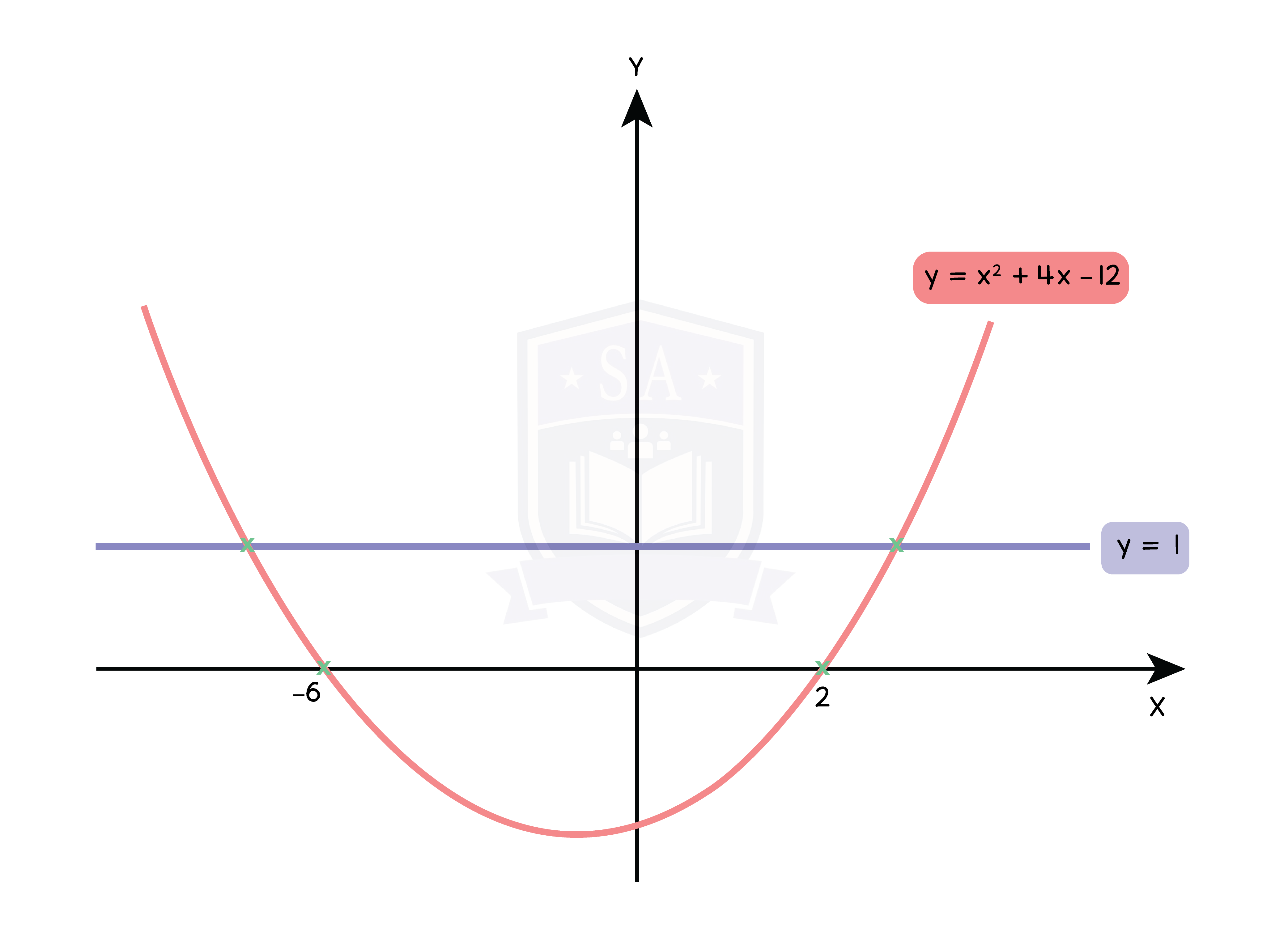
Type 1: 2 Linear Equations
Type 2: Quadratic and Linear Equation
Part 2: Remainder Theorem
If a polynomial f(x) is divided by (ax – b), the remainder is f(b/a).

