REVISION NOTES
IGCSE Edexcel Further Pure Mathematics
1.1 Logarithmic Functions and Indices
1.1.1 The functions ax and logb x (where b is a natural number greater than one)
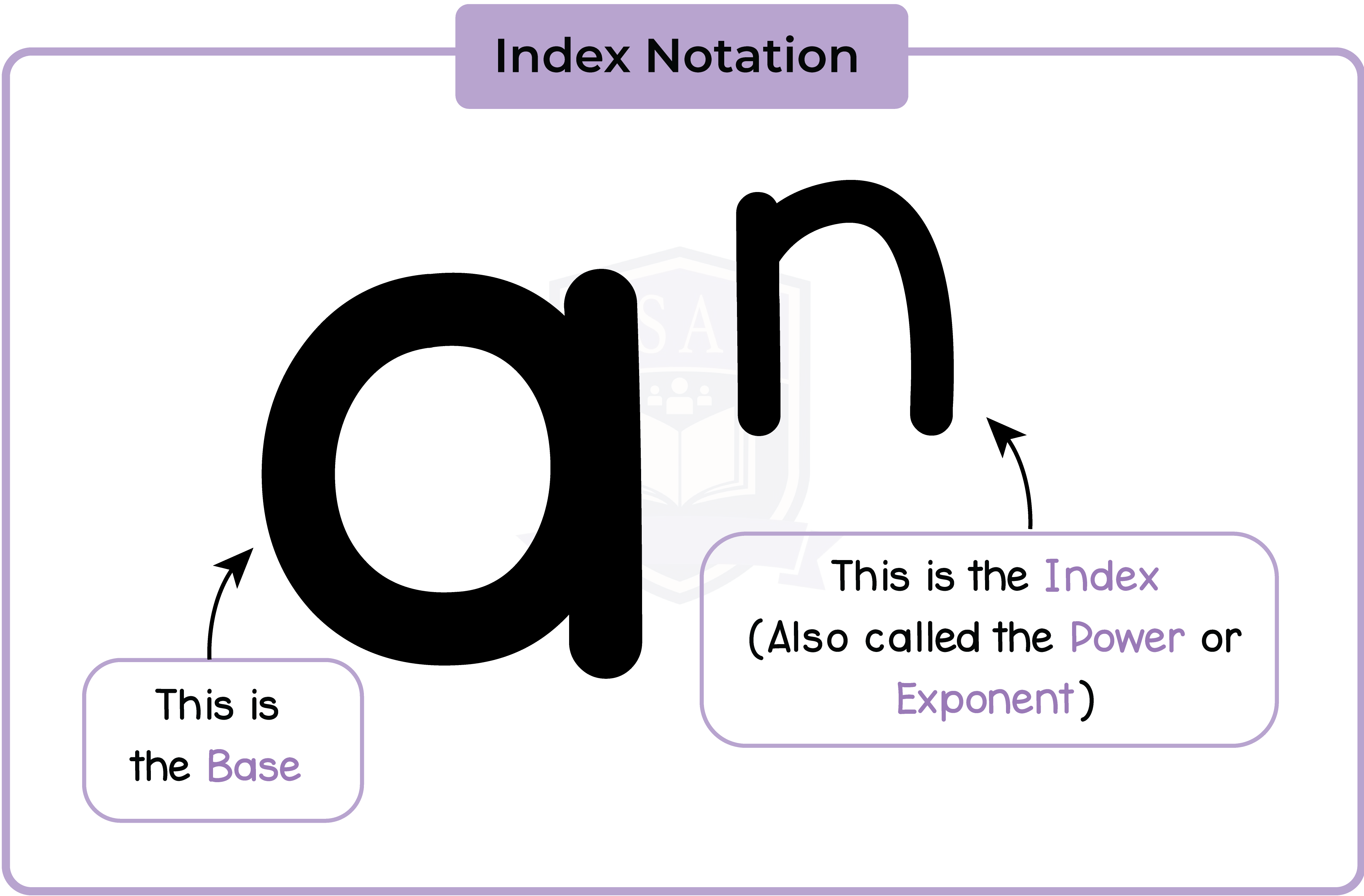
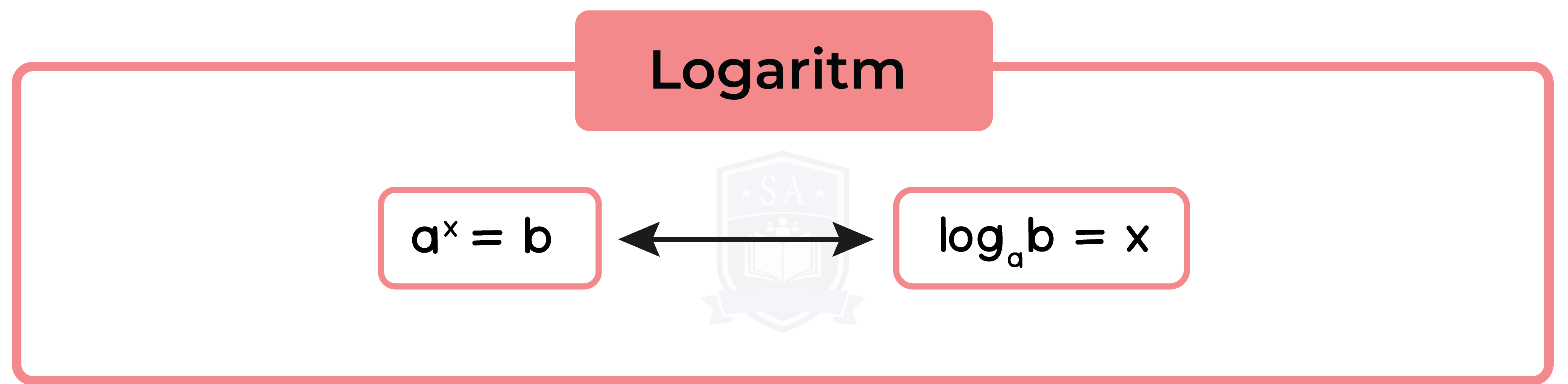
1.1.2 Use properties of indices and logarithms, including change of base
For example log232 = 5 means that 25 = 32
In words, you would say ‘the logarithm of 32, to base 2, is 5
To remove log, solve for x:
- On one side: use concept of log to remove
- E.g. log2x = 4 → x = 24 = 16
- On two sides: use change of base law (rule 8 above), to make both logarithms have the same base, then cancel out log
- When solving log in quadratic: make “logab = x” to solve as a normal quadratic, then replace values of “x” to equal “logab”
Natural log
loge = ln
Always keep final answer always in ln
1.1.3 Simple manipulation of surds
1.1.4 Rationalising the denominator
