REVISION NOTES
1.5.1 Write word equations and balanced chemical equations (including state symbols):
State symbols used in chemical equation:

WORD EQUATION
Sodium + Hydrochloric acid → Sodium chloride + Hydrogen
BALANCED CHEMICAL EQUATION
2Na + 2HCl → 2NaCl + H2
LAW OF CONSERVATION
1.5.2 Calculate relative formula masses (including relative molecular masses) (Mr) from relative atomic masses (Ar)
RELATIVE ATOMIC MASS (AR)
RELATIVE FORMULA MASS (MR)
EXAMPLE
What is the relative formula mass (Mr) of a water molecule (H2O)?
Ar of H = 1
Ar of O = 16
Mr of H2O = H x 2 + O x 1
= 1 x 2 + 16 x 1
= 18
1.5.3 Know that the mole (mol) is the unit for the amount of a substance
MOLE (SYMBOL:N)
AVOGADRO’S CONSTANT
MOLAR MASS
1.5.4 Understand how to carry out calculations involving amount of substance, relative atomic mass (Ar) and relative formula mass (Mr)
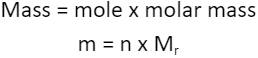
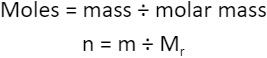
Molar mass can be:
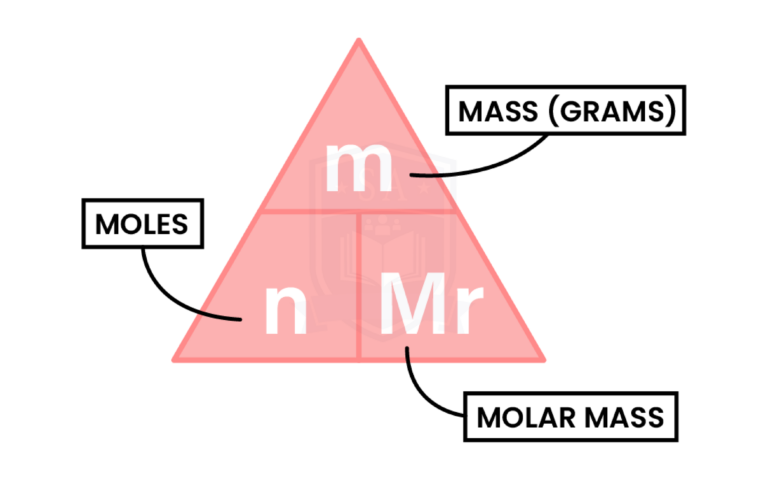
EXAMPLE
How many moles are there in 64g of O2?
1.5.5 Calculate reacting masses using experimental data and chemical equations
Information of moles can be obtained from chemical equations
2Na + 2HCl → 2NaCl + H2
Information 1:
Every 2 moles of Na react with 2 moles of HCl to produce 2 moles of NaCl and 1 mole of H2
Information 2:
0.5 mole of Na reacts with 0.5 mole of HCl to produce 0.5 mole of NaCl and 0.25 mole of H2
The number of moles reacted do not have to be whole numbers
Information 3:
mole of Na : HCl : NaCl : H2 = 2 : 2 : 2 : 1
The coefficients in chemical equations show the simplest mole ratio
REACTING MASS
Masses of reactants and products can be calculated from balanced chemical equation:
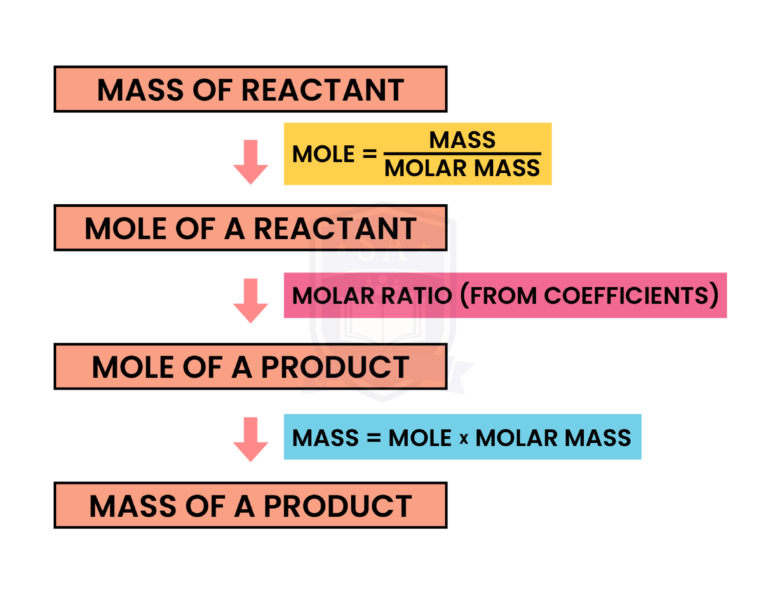
EXAMPLE
If 34.5 grams of sodium metal is completely reacted with excess hydrochloric acid, how many grams of hydrogen gas will be produced according to the following reaction?
2Na + 2HCl → 2NaCl + H2
Given: mass (Na) = 34.5g
Calculate: mass (H2)
STEP 1: FIND THE MOLE OF NA
Mole (Na) = mass (Na) ÷ Mr (Na)
= 34.5g ÷ 23
= 1.5 mol
STEP 2: FIND THE MOLE OF H2 PRODUCED
Mole (Na) : Mole (H2) = 2 : 1
(this can be found from the coefficients in the balanced chemical equation)
If mole (Na) = 1.5 mol from step 1
Then mole (H2) = 1.5 ÷ 2 = 0.75 mol
STEP 3: FIND THE MASS OF H2 PRODUCED
Mass (H2) = mole (H2) x Mr (H2)
= 0.75 mol x (1 x 2)
= 0.75 x 2
= 1.5 grams
1.5.6 Calculate percentage yield
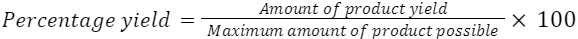
In practice, you never get 100% yield in a chemical process for several reasons
1.5.7 Understand how the formulae of simple compounds can be obtained experimentally, including metal oxides, water and salts containing water of crystallisation
CASE 1: METAL OXIDES(MAGNESIUM OXIDE)
EXAMPLE
Some magnesium (Mg) was heated in a crucible to form magnesium oxide. Use the following information to deduce the formula of magnesium oxide.
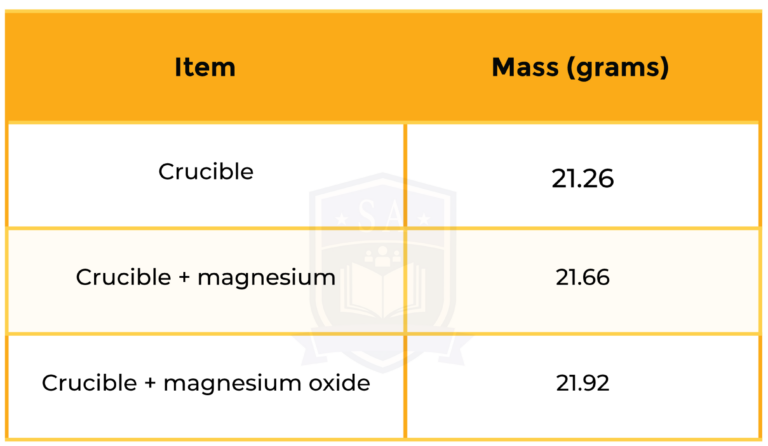
STEP 1: MASS OF MAGNESIUM
Mass of Mg = mass (crucible + magnesium) – mass (crucible)
= 21.66 – 21.26
= 0.40 grams
STEP 2: MASS OF OXYGEN
Mass of O = mass (crucible + magnesium oxide) – mass (crucible + magnesium)
= 21.92 – 21.66
= 0.26 grams
Step 3: mole ratio of Mg and O
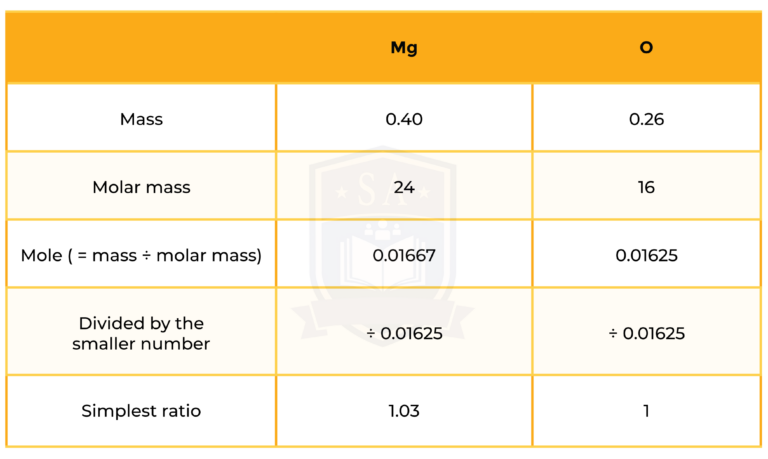
So the formula is MgO.
CASE 2: WATER OF CRYSTALLISATION
EXAMPLE
11.25 g of hydrated copper sulphate, CuSO4・xH2O, is heated until it loses all of its water. Its new mass is found to be 7.19 g. What is the value of x?
STEP 1: MASS OF WATER
Mass of water = mass of hydrated salt – mass of anhydrous salt
= 11.25 – 7.19
= 4.06 grams
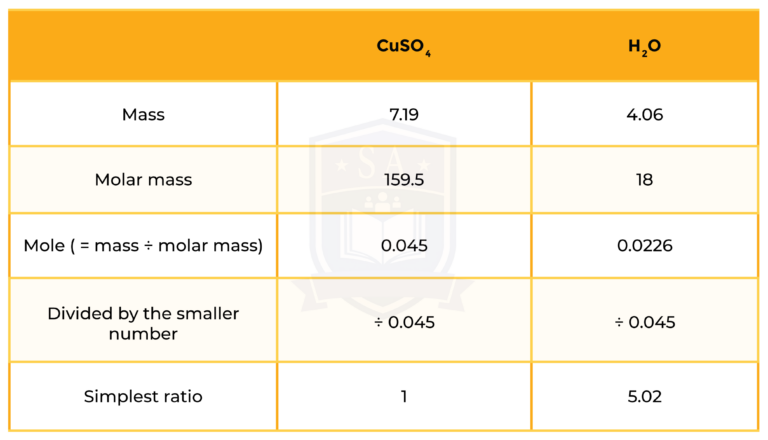
So the formula is CuSO4・5H2O, the value of x is 5.
1.5.8 Know what is meant by the terms empirical formula and molecular formula
EXPIRICAL FORMULA
MOLECULAR FORMULA
Example

1.5.9 Calculate empirical and molecular formulae from experimental data
CALCULATION OF EMPIRICAL FORMULA
EXAMPLE
0.150 g of copper reacts with oxygen from 0.188 g of copper oxide. Find the empirical formula of copper oxide.
So the empirical formula of copper oxide is CuO.
CALCULATION OF MOLECULAR FORMULA
EXAMPLE
The empirical formula of a compound of boron and hydrogen is BH3. Its molar mass is 28g/mol . Determine the molecular formula of the compound.

So the molecular formula of the compound is B2H6.
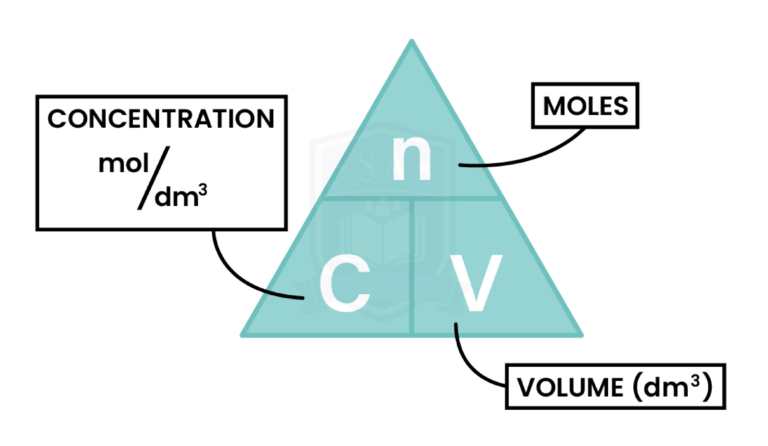
1.5.10C Understand how to carry out calculations involving amount of substance, volume and concentration (in mol/dm³) of solution
CONCENTRATION OF SOLUTION
Solution consists of:
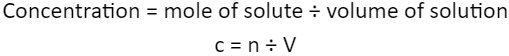
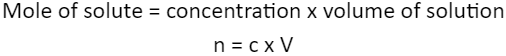
EXAMPLE
0.03 mol of sodium carbonate (Na2CO3) is dissolved in 300 cm3 of water. Calculate the concentration of the solution.
Volume in dm3 = 300 cm3 ÷ 1000 = 0.3 dm3
Concentration = mole of solute ÷ volume of solution
= 0.03 mol ÷ 0.3 dm3
= 0.1 mol/dm3
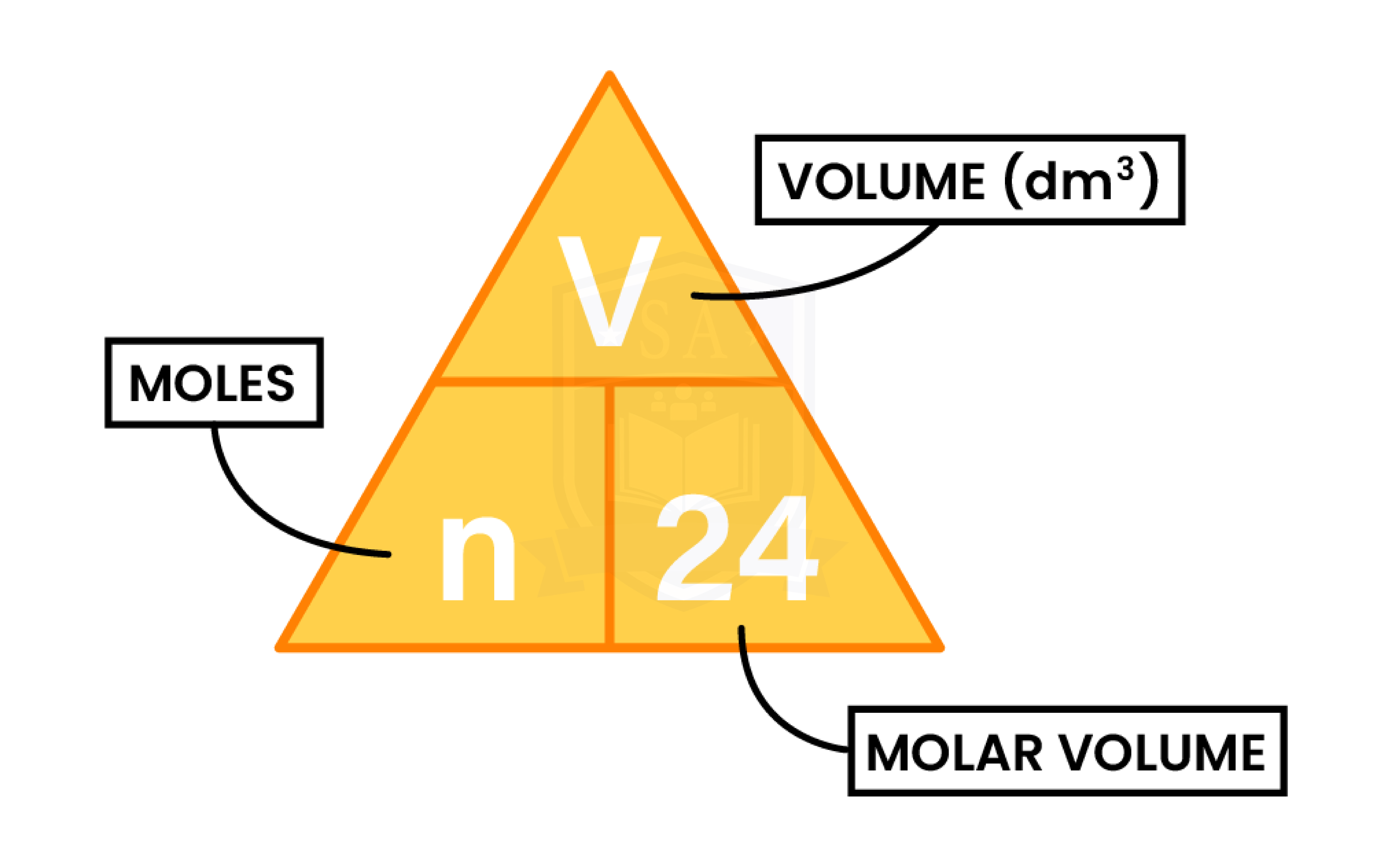
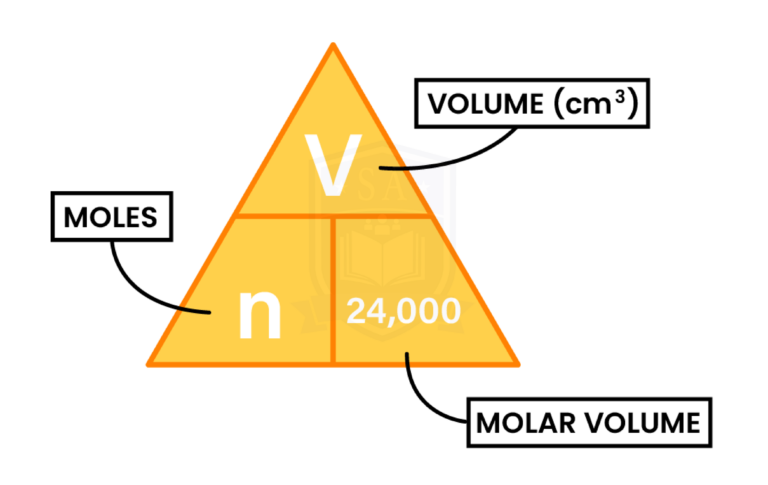
1.5.11C Understand how to carry out calculations involving gas volumes and the molar volume of a gas (24 dm3 and 24 000 cm3 at room temperature and pressure (rtp))
VOLUME AND MOLE OF A GAS
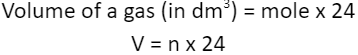
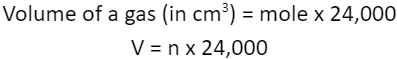
EXAMPLE
Calculate the volume at rtp in cubic centimetres (cm3), of 3 mol of oxygen, O2.
Volume (in cm3) = mole x 24,000
= 3 x 24,000
= 72,000 cm3
1.5.12 Practical: know how to determine the formula of a metal oxide by combustion (e.g. magnesium oxide) or by reduction (e.g. copper(II) oxide)
FORMULA OF METAL OXIDE BY COMPOSITION
FORMULA OF METAL OXIDE BY REDUCTION
EXAMPLE
An oxide of copper was reduced to copper metal by reaction with hydrogen.
copper oxide + hydrogen → copper + water
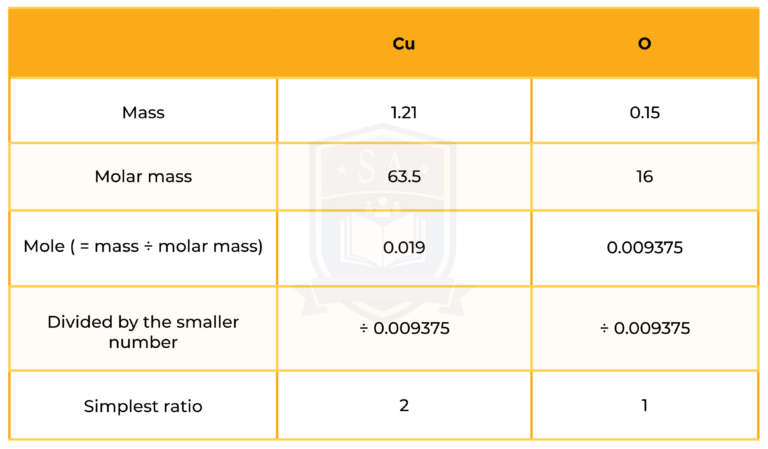
Use the data in the table to find the empirical formula of this oxide of copper.
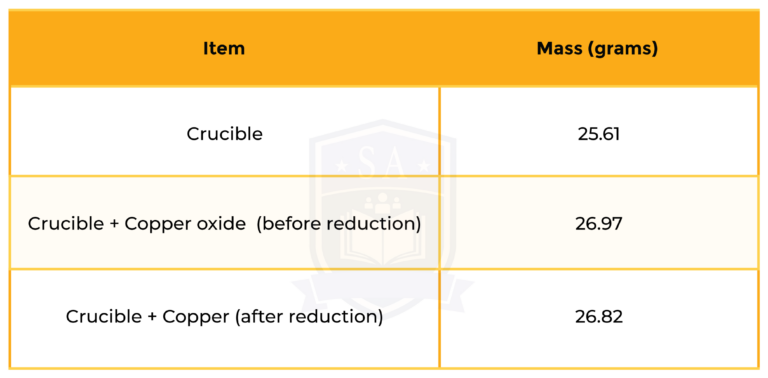
STEP 1: MASS OF COPPER
Mass of Mg = mass (crucible + copper) – mass (crucible)
= 26.82 – 25.61
= 1.21 grams
STEP 2: MASS OF OXYGEN
Mass of O = mass (crucible + copper oxide) – mass (crucible + copper)
= 26.97 – 26.82
= 0.15 grams
Step 3: mole ratio of Cu and O

So the formula is Cu2O.

© 2025 Studia Academy. All rights reserved.